Неперервні випадкові величини. Щільність розподілу

Як уже згадувалось в розділі 6.1, під неперервною випадковою величиною слід розуміти випадкову величину, яка може приймати будь-яке числове значення з деякого скінченого або нескінченного інтервалу (а;в).

Головна різниця в задачах обчислення ймовірностей для дискретних і неперервних випадків полягає в тому, що в дискретному випадку шукається ймовірність типу Х=с (випадкова величина прийме конкретне значення), а у випадку неперервної величини ймовірність такого типу дорівнює нулю, тому для її повної характеристики водять поняття інтегральної та диференціальної функції розподілу, а цікавими для нас є ймовірності подій типу а £Х£ в (випадкова величина прийме значення з деякого проміжку). При цьому:

р (а £Х£ в)= р (а <Х£ в)= р (а £Х< в)= р (а <Х< в)

Означення. Інтегральною функцією розподілу випадкової величини Х називають функцію F(X), яка визначає ймовірність того, що випадкова величина Х прийме значення менші х (х R), тобто

F(X) = P(X < x) (16)

Властивості інтегральної функції розподілу

1. 0≤ F(X) ≤1.

2. Функція розподілу є неспадною: якщо х₁<х₂, то F(х₁) < F(х₂).

3. Ймовірність попадання випадкової величини Х в інтервал (а;в) < .

4. Функція розподілу неперервна зліва: .

5. або < .

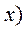6. ; .

Має місце факт: ймовірність події а £Х£ в рівна площі фігури, обмеженої прямими у =0, х = а, х = в і графіком функції . Тобто справедлива рівність

р (а £Х£ в)= , для будь-яких а і в, а£в.

Ця рівність виконується і для загального випадку, якщо невід’ємна.

Таким чином, функція дозволяє обчислити ймовірності, пов’язані з випадковою величиною Х, тобто задає закон розподілу НВВ Х, а функцію називають диференціальною функцією розподілу або щільністю ймовірностей.