Рівень А. 1. Випадковою називають величину, яка

1. Випадковою називають величину, яка

1) в результаті випробування приймає одне і тільки одне можливе дійсне значення, наперед невідоме і залежне від випадкових обставин.

2) при умовах що розглядаються може здійснитися, а може й не здійснитися.

3) в результаті випробування приймає скінчену або нескінчену кількість значень, наперед невідомих

2. Випадкова величина Х називається дискретною,

1) яка може приймати відокремлені ізольовані одне від одного числові значення з відповідними ймовірностями..

2) якщо її функцію розподілу можна подати у вигляді

F (x)= , де – диференціальна функція розподілу.

3) яка може приймати будь-яке числове значення з деякого скінченого або нескінченного інтервалу (а;в).

3. Співвідношення, що встановлює зв’язок між можливими значеннями випадкової величини та їх ймовірностями називається...(вкажіть невірну відповідь)

1) законом розподілу випадкової величини;

2) щільністю випадкової величини;

3) числовою характеристикою випадкової величини.

4. Чи справедлива нерівність

1) так;

2) ні.

5. Числовою характеристикою випадкових величин не є:

1) математичне сподівання;

2) середнє квадратичне відхилення;

3) закон розподілу.

6. Чи справедлива нерівність

1. так;

2. ні.

7. Імовірність того, що випадкова величина Х прийме значення менше х, називають:

1) інтегральною функцією розподілу;

2) диференційованою функцією розподілу;

3) неперервною функцією розподілу.

8. Диференційованою функцією розподілу неперервної випадкової величини називають:

1) первісну від її інтегральної функції розподілу;

2) похідну від її інтегральної функції розподілу;

3) похідну першого порядку від її інтегральної функції розподілу.

9. Дисперсію дискретної випадкової величини Х доцільно знаходити за формулою…

1) D(Х)=M((Х-M(Х))²);

2) D(Х)=M(Х²)-(M(Х))²;

3) D(Х)=(σ(Х))².

10. Математичне сподівання дискретної випадкової величини обчислюють за формулою:

1) М(Х)= ;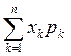

2) М(Х)= ;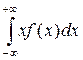

3) D(X)=M(X²)-(M(X))².

Поиск по сайту: