Точкова оцінка математичного сподівання

Нехай х₁, х₂, х₃,..., х_n – вибірка отримана в результаті п незалежних випробувань над випадковою величиною Х – деякою ознакою генеральної сукупності, яка має математичне сподівання М(Х)= а.

За точкову оцінку математичного сподівання а =М(Х) беруть вибіркове середнє .

Легко довести, що є незміщеною для М(Х)= а, тобто М()= а.

Якщо додатково припустити, що випадкова величина Х має скінчену дисперсію , тоді можна стверджувати, що оцінка є змістовною. Якщо обчислити дисперсію вибіркової середньої , то отримаємо

.

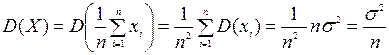Оскільки 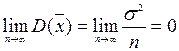, то це означає, що оцінка є змістовною для параметра а.

Твердження. Якщо випадкова величина Х нормально розподілена з параметрами М(Х)=а і , то оцінка має у класі всіх незміщених оцінок математичного сподівання а мінімальну дисперсію, яка дорівнює . Тому є ефективною оцінкою параметра а.

Поиск по сайту: