Перевірка гіпотези про рівність часток ознаки двох сукупностей

Задача порівняння часток (відносних частот) ознаки в двох сукупностях досить часто зустрічається на практиці. Наприклад, якщо вибіркова частка ознаки однієї сукупності відрізняється від такої ж частки в другій сукупності, чи вказує це на те, що наявність ознаки в одній сукупності дійсно ймовірніше, чи ця різниця часток є випадковою?

Сформулюємо задачу. Маємо дві сукупності, генеральні частки ознаки яких дорівнюють відповідно р₁ і р₂. Необхідно перевірити нульову гіпотезу про рівність генеральних часток, тобто Н₀: р₁ = р₂. Для перевірки гіпотези Н₀ із цих сукупностей взяті дві незалежні вибірки достатньо великого об’єму п₁ і п₂. Вибіркові частки ознаки рівні відповідно і 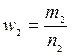, де т₁ і т₂ – відповідне число елементів першої і другої вибірки, що має дану ознаку.

При достатньо великих п₁ і п₂, вибіркові частки і мають наближено нормальний закон розподілу з математичним сподіванням р₁ і р₂ і дисперсіями і , тобто відповідно N (р₁; ) і N (р₂; ).

При справедливості гіпотези Н₀: р₁ = р₂ = р різниця - має нормальний закон розподілу з математичним сподіванням М( ‑ )= р‑р= 0і дисперсією .Тому статистика

має стандартний нормальний розподіл N(0;1)

В якості невідомого значення р що входить у вираз статистики t, беруть його найкращу оцінку , рівну вибірковій частці ознаки, якщо дві вибірки з’єднати в одну, тобто .

Вибір виду критичної області і перевірка гіпотези здійснюється таким же чином, як і вище, при перевірці гіпотези про рівність середніх.

Приклад. Контрольну роботу з математичної статистики по індивідуальним варіантам виконували студенти двох груп першого курсу. В першій групі було запропоновано 105 задач, з яких правильно розв’язано 60, у другій із 140 запропонованих правильно розв’язано 69. На рівні значимості 0,02 потрібно перевірити гіпотезу про відсутність суттєвої різниці в засвоєнні навчального матеріалу студентами обох груп.

Розв’язання

Припустимо, що частки розв’язаних задач студентами обох груп рівні, тобто Н₀: р₁ = р₂ = р. В якості альтернативної візьмемо гіпотезу Н₁: р₁ ¹ р₂. При справедливості гіпотези Н₀ найкращою оцінкою р буде

= . Вибіркові частки розв’язаних задач для кожної групи і . Статистику критерію обчислимо за формулою:

При конкуруючій гіпотезі Н₁: р₁ ¹ р₂ обираємо критичну двосторонню область: Ф(t_кр)=1-0,02=0,98, звідки за таблицею значень функції Лапласа t_кр= t_0,98=2,33. Фактичне значення критерію менше критичного, тобто t<t_0.98. Отже, гіпотеза Н₀ приймається, тобто отримані дані не протирічать гіпотезі про однаковий рівень засвоєння навчального матеріалу студентами обох груп.

Поиск по сайту: