Теорема множення ймовірностей залежних подій

Якщо події А і В залежні, то ймовірність добутку цих подій дорівнює добутку ймовірностей однієї з них на умовну ймовірність іншої, за умови, що перша подія відбулася, тобто

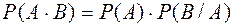або (2)

Наслідок. Ймовірність добутку скінченої кількості залежних подій обчислюється за формулою

Задача 13. Студент прийшов на екзамен, знаючи лише 20 з 25 екзаменаційних питань. Яка ймовірність того, що він знає відповіді на всі три запитання?

Розв’язання Випробування – студент отримає три запитання.

подія А₁ – студент знає відповідь на перше запитання;

подія А₂ – студент знає відповідь на друге запитання;

подія А ₃ –студент знає відповідь на третє запитання.

Оскільки студент знає відповіді лише на 20 запитань із 25, то події А₁, А₂, А₃ – залежні. Тому для розв’язання задачі скористаємося формулою (2) для випадку трьох залежних подій

.

Маємо .

Відповідь: 0,49.

Зауваження. Теореми множення ймовірностей використовуються для того, щоб дати відповідь на запитання: „Події, що розглядаються, залежні чи ні?”

У випадку залежності подій спрацьовує формула (2), у випадку незалежних подій – формула (1).

Приклад. З колоди 36 карт навмання виймають одну карту. Припустимо здійснення таких подій:

подія А – взята карта пікова;

подія В – взята карта дама.

Визначимо залежні події чи ні? Для цього розглянемо добуток подій А і В – подію АВ: „взята карта пікова дама”.

Знайдемо ймовірність подій А, В та АВ:

Р(А)= ; Р(В)= 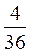; Р(АВ)= .

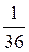Відповідно до зауваження, якщо події А і В незалежні, то справедливою буде рівність , а якщо залежні, то ця рівність не виконуватиметься. Перевіряємо її, підставляючи значення ймовірностей,

Рівність справедлива, отже події А і В – незалежні.

Поиск по сайту: