 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
а) відношенню кількості елементарних подій, що сприяють події до кількості всіх
приклад розв'язання
1. Інвестиційна кампанія має 12 пакетів акцій, серед яких 7 пакетів цукрових заводів. Визначити ймовірність, що серед навмання вибраних 5 пакетів акцій є рівно 3 пакети цукрових заводів.
Розв'язування:
Подія  ― серед навмання вибраних 5 пакетів акцій є 3 пакети цукрових заводів.
― серед навмання вибраних 5 пакетів акцій є 3 пакети цукрових заводів.
Використовуємо класичне означення ймовірності:
 , де
, де  ,
,
 , (12-7=5― пакети не цукрових заводів).
, (12-7=5― пакети не цукрових заводів).
Отже, 
2. В двох партіях відповідно 82% і 45% якісних виробів. Навмання вибирають по одному виробу із кожної партії. Яка ймовірність виявити серед них: а) хоча б один бракований виріб; б) два бракованих вироби; в) один бракований та один якісний вироби?
Розв'язування:
 ― ймовірність того, що виріб якісний, якщо він з першої партії;
― ймовірність того, що виріб якісний, якщо він з першої партії;
 ― ймовірність того, що виріб якісний, якщо він з другої партії.
― ймовірність того, що виріб якісний, якщо він з другої партії.
Ймовірності того, що вироби браковані, відповідно дорівнюють:  .
.
а) подія  ― серед двох виробів хоча б один бракований;
― серед двох виробів хоча б один бракований;
протилежна подія  ― обидва вироби якісні, тоді
― обидва вироби якісні, тоді
 .
.
б) подія  ― обидва вироби браковані:
― обидва вироби браковані:
 .
.
в) подія 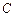 ― один виріб бракований і один якісний:
― один виріб бракований і один якісний:
 .
.
3. В магазин надходять однотипні вироби з трьох заводів: 30%― з першого заводу, 60%― з другого, 10%― з третього. Серед виробів першого заводу 70% виробів першого сорту, серед виробів другого і третього заводів відповідно 90% і 80% виробів першого сорту. Куплено один виріб. Він виявився виробом першого сорту. Знайти ймовірність того, що куплений виріб виготовлений на другому заводі.
Розв'язування:
Для знаходження відповідної ймовірності потрібно використати формулу Байєса.
Описуємо гіпотези: 
 ― виріб, виготовлений на
― виріб, виготовлений на  -ому заводі.
-ому заводі.
Ймовірності гіпотез відповідно дорівнюють:

Подія  ― куплений виріб є виробом першого сорту. Обчислюємо умовні ймовірності:
― куплений виріб є виробом першого сорту. Обчислюємо умовні ймовірності:

Згідно з умовою задачі, потрібно знайти  ― ймовірність того, що куплений виріб першого сорту виготовлений на другому заводі. За формулою Байєса:
― ймовірність того, що куплений виріб першого сорту виготовлений на другому заводі. За формулою Байєса:

4. Ймовірність виконання договору для кожного з трьох ( ) заводів дорівнює 0,9 (
) заводів дорівнює 0,9 ( ). Скласти закон розподілу випадкової величини
). Скласти закон розподілу випадкової величини 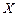 ― числа заводів, які виконають договір.
― числа заводів, які виконають договір.
Розв'язування:
Закон розподілу випадкової величини 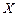 записуємо у вигляді таблиці, ймовірності
записуємо у вигляді таблиці, ймовірності  обчислюємо за формулою Бернуллі:
обчислюємо за формулою Бернуллі:


| ||||

| 0,001 | 0,027 | 0,243 | 0,729 |

Контроль:  .
.
5. Внаслідок маркетингових досліджень встановлено, що ймовірність реалізації одиниці продукції становить 0,6. Знайти ймовірність, що з 200 вироблених одиниць продукції буде реалізовано: а) рівно 130; б) не більше 70% з 200 одиниць; в) від 120 до 150 одиниць; г) обчислити найімовірніше число реалізованих одиниць.
Розв'язування:
Для знаходження відповідних ймовірностей використовуємо локальну та інтегральну теореми Лапласа:
а) за умовою задачі 
 , де
, де 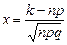 .
.
Обчислюємо значення  :
:
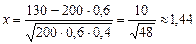 .
.
Використовуючи таблицю значень функції  , знаходимо
, знаходимо
 , тоді
, тоді
 .
.
б) Подія  ― буде реалізовано не більше 70% продукції (140 одиниць становить 70%),
― буде реалізовано не більше 70% продукції (140 одиниць становить 70%),

Згідно з інтегральною теоремою Лапласа:
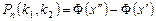 , де
, де 
 ,
,
 (функція протабульована).
(функція протабульована).
В даному випадку 
Обчислюємо значення  :
:

тоді:  .
.
в) За допомогою інтегральної теореми Лапласа знаходимо
 ,
,
тоді:
 .
.
г) Найімовірніше число реалізованих одиниць продукції  знаходимо з нерівності:
знаходимо з нерівності:

отже, 
Зауваження: Якщо  потрібно використовувати формулу Бернуллі:
потрібно використовувати формулу Бернуллі:  .
.
6. Задана функція розподілу ймовірностей прибутку підприємця:

Потрібно знайти: а) математичне сподівання та середнє квадратичне відхилення прибутку підприємця; б) ймовірність, що прибуток підприємця прийме значення з інтервалу (3;4).
Розв'язування:
Знаходимо густину розподілу ймовірностей  :
:

а) Математичне сподівання обчислюємо за формулою:  .
.
 Обчислюємо дисперсію
Обчислюємо дисперсію 


Середнє квадратичне відхилення прибутку підприємця  , отже,
, отже, 
б) Ймовірність того, що прибуток підприємця набуде значення із заданого інтервалу, обчислюємо за формулою:

В даному випадку:

7. Задана генеральна сукупність. Знайти вибірку з 20 елементів підряд, починаючи з першого, та виконати такі вправи:
1) побудувати статистичний розподіл вибірки та його емпіричну функцію розподілу;
2) обчислити числові характеристики вибірки;
3) побудувати полігон частот та гістограму, розбивши інтервал на 5 рівних підінтервалів;
4) знайти моду, медіану, розмах та коефіцієнт варіації.
16, 12, 9, 11, 8, 16, 18, 12, 8, 18, 14, 16, 11, 15, 21, 19, 11, 14, 16, 18, 15, 9, 14, 16, 12, 13, 17, 19, 13. 17. 14. 11. 12, 13, 8, 10, 9, 11, 10, 17, 13, 18, 16, 21, 9, 14, 15.
Розв`язання:
Утворюємо вибірку, що складається з 20 елементів генеральної сукупності
16, 12, 9, 11, 8, 16, 18, 12, 8, 18, 14, 16, 11, 15, 21, 19, 11, 15, 21, 19 і за нею будуємо статистичний розподіл:

| ||||||||||

|
з якого і будуємо емпіричну функцію розподілу, яка визначається за формулою  :
:

Побудуємо графік функції 

2). Обчислюємо числові характеристики за формулами:


3). Будуємо полігон частот:

Гістограму будуємо з кроком  . Для цього спочатку запишемо інтервальний ряд
. Для цього спочатку запишемо інтервальний ряд
| 
| 
| 
| 
| 
|

| |||||

| 
| 
| 
| 
| 
|

4). Мода (варіанта, яка має найбільшу частоту):  .
.
Медіана (варіанта, яка ділить варіаційний ряд навпіл):  .
.
Розмах варіації:  .
.
Коефіцієнт варіації:  .
.
8. Зв’язок ознак Х та Y подається кореляційною таблицею:
| Y X | 
| ||||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||

|
Записати рівняння прямої регресії.
Рішення. Переходимо до умовних варіант  , тобто С1=45, С2=38, h1=5, h2=10 (С1, С2 – варіанти, що мають найбільшу частоту 35).
, тобто С1=45, С2=38, h1=5, h2=10 (С1, С2 – варіанти, що мають найбільшу частоту 35).
| V U | -3 | -2 | -1 | 
| |||
| -2 | - | - | - | - | |||
| -1 | - | - | - | - | |||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | |||||

|
Послідовно знаходимо:

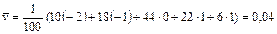 ;
;
 ;
;
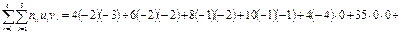
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Рівняння прямої регресії Y та Х має вигляд:

або  .
.
Г.
2 Сумою двох випадкових подій є подія, яка полягає в тому, що:
а) відбулися обидві події; б) відбулася тільки одна з двох подій;
в) відбулася хоча б одна з двох подій; г) не відбулася одна з подій; д) інша відповідь.
В.
3 Добутком двох випадкових подій є подія, яка полягає в тому, що:
а) відбулися обидві події; б) відбулася тільки одна з двох подій;
в) відбулася хоча б одна з двох подій; г) не відбулася одна з подій; д) інша відповідь.
А.
4 Протилежною до суми двох подій є подія, яка полягає в тому, що:
а) не відбулася хоча б одна із подій; б) не відбулися обидві події;
в) одна подія відбулася, а інша ні; г) відбулася хоча б одна із подій; д) інша відповідь.
Б.
5 Протилежною до добутку двох подій є подія, яка полягає в тому, що:
а) відбулася хоча б одна із подій; б) не відбулися обидві події;
в) одна подія відбулася, а інша ні; г) не відбулася хоча б одна із подій; д) інша відповідь.
Г.
6 Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2) 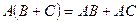 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
а) 1, 2, 3 і 5; б) 1, 2 і 5; в) 2, 3 і 4; г) 1 і 5; д) інша відповідь.
Б.
7 Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1) 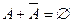 ; 2)
; 2) 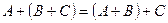 ; 3)
; 3) 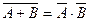 ;
;
4)  ; 5)
; 5)  .
.
а) 1, 2 і 5; б) 2 і 4; в) 2 і 3; г) 2, 3, 4 і 5; д) інша відповідь.
В.
8 Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) 2, 3, 4 і 5; б) всі; в) 1, 3 і 5; г) 2 і 3; д) інша відповідь.
Д.
9 Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ; 5)
; 5)  .
.
а)1, 2, 3 і 4; б) 3, 4 і 5; в) 1 і 2; г) 1 і 4; д) інша відповідь.
Г.
10 Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) 3, 4 і 5; б) 2, 3 і 4; в) 1, 2, 3 і 4; г) 3 і 5; д) інша відповідь.
А.
11 Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2) 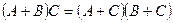 ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) 1, 3, 4 і 5; б) 2 і 3; в) 3 і 5; г) 1 і 4; д) інша відповідь.
В.
12 Нехай  - довільні події,
- довільні події,  - простір всіх елементарних подій,
- простір всіх елементарних подій,  - неможлива подія. Вкажіть, які із співвідношень правильні:
- неможлива подія. Вкажіть, які із співвідношень правильні:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5) 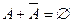 .
.
а) 1, 2, 3 і 4; б) 1, 3 і 4; в) 2, 3 і 5; г) 1, 2 і 5; д) інша відповідь.
Б.
13 Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулися події
- довільні події. Вкажіть формулу, яка відповідає події: відбулися події  і
і 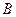 , але не відбулася подія
, але не відбулася подія 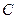 .
.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
14 Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулася подія
- довільні події. Вкажіть формулу, яка відповідає події: відбулася подія  , а події
, а події 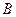 та
та 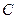 не відбулися.
не відбулися.
а)  ; б)
; б) 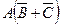 ; в)
; в) 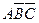 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
15 Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулася тільки одна із цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулася тільки одна із цих подій.
а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
16 Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулися рівно дві з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулися рівно дві з цих подій.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
17 Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулися всі три з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулися всі три з цих подій.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь
; д) інша відповідь
Б.
18 Нехай  - довільні події. Вкажіть формулу, яка відповідає події: не відбулася жодна з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: не відбулася жодна з цих подій.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
19 Нехай  - довільні події. Вкажіть формулу, яка відповідає події: відбулася принаймні одна з цих подій.
- довільні події. Вкажіть формулу, яка відповідає події: відбулася принаймні одна з цих подій.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
20 Ймовірність суми двох подій  і
і 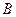 обчислюється за формулою:
обчислюється за формулою:
а)  ; б)
; б)  ;
;
в) 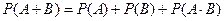 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
21 Ймовірність добутку несумісних подій дорівнює:
а) добутку ймовірностей цих подій; б) сумі ймовірностей цих подій;
в) нулю; г) одиниці; д) інша відповідь.
В.
22 Ймовірність добутку незалежних подій дорівнює:
а) відношенню ймовірностей цих подій; б) сумі ймовірностей цих подій;
в) нулю; г) одиниці; д) інша відповідь.
Д.
23 Протилежна подія має ймовірність, що в сумі з ймовірністю даної події дорівнює:
а) 2; б) 1.5; в) 1; г) 0.5; д) інша відповідь.
В.
24 Ймовірність події  , що сприяє події
, що сприяє події 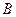 є:
є:
а) меншою за ймовірність 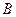 ; б) не більшою за ймовірність
; б) не більшою за ймовірність 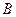 ;
;
в) більшою за ймовірність 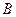 ; г) не меншою за ймовірність
; г) не меншою за ймовірність 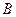 ; д) інша відповідь.
; д) інша відповідь.
Б.
25 Класичне означення ймовірності можна застосувати, коли:
а) простір елементарних подій скінченний; б) завжди;
в) простір елементарних подій складається з рівноможливих елементів;
г) простір елементарних подій містить скінченну кількість рівноможливих елементів; д) інша відповідь
Г.
26 Геометричне означення ймовірності можна застосовувати, коли:
а) простір елементарних подій задається множиною евклідового простору;
б) простір елементарних подій задається множиною евклідового простору із скінченною мірою;
в) простір елементарних подій задається множиною евклідового простору із скінченною мірою та всі елементарні події рівноможливі;
г) простір елементарних подій задається множиною евклідового простору та всі елементарні події рівноможливі;
д) інша відповідь.
В.
27 Згідно класичного означення ймовірності, ймовірність події дорівнює:
а) відношенню кількості елементарних подій, що сприяють події до кількості всіх
рівноможливих елементарних подій;
б) відношенню кількості всіх рівноможливих елементарних подій до кількості елементарних подій, що сприяють події;
в) добутку кількості елементарних подій, що сприяють події та кількості всіх рівноможливих елементарних подій;
г) кількості елементарних подій, що сприяють події; д) інша відповідь.
А.
28 Згідно геометричного означення ймовірності, ймовірність події дорівнює:
а) геометричній мірі множини, що задає подію;
б) частці від ділення геометричної міри множини, що задає подію на геометричну міру множини, що задає весь простір елементарних подій;
в) відношенню міри простору елементарних подій до міри події;
г) процентному вмісту події в просторі елементарних подій; д) інша відповідь.
Б.
29 Згідно теореми множення ймовірностей ймовірність добутку двох подій дорівнює:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
30 Ймовірність добутку трьох подій обчислюється за формулою:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
31 Повною групою подій є:
а) набір незалежних рівноймовірних подій;
б) набір несумісних подій, сума яких є достовірною подією;
в) набір незалежних подій, сума яких є достовірною подією;
д) набір подій, сума яких є достовірною подією; д) інша відповідь.
Б.
32 Група подій називається незалежною в сукупності, якщо:
а) кожні дві події з цієї групи незалежні;
б) ймовірність добутку будь-якого скінченого набору подій з групи дорівнює добутку їх ймовірностей;
в) ймовірність добутку всіх подій групи дорівнює добутку їх ймовірностей;
г) ймовірність добутку подій групи дорівнює нулю; д) інша відповідь.
Б.
33 За формулою повної ймовірності ймовірність події  дорівнює (
дорівнює (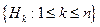 –повна група подій):
–повна група подій):
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
34 Формула Байєса має вигляд ( –повна група подій):
–повна група подій):
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Д.
35 Апостеріорні ймовірності гіпотез можна обчислити за формулою:
а) Байєса; б) Бернуллі; в) Пуассона; г) повної ймовірності; д) інша відповідь.
А.
36 Схемою Бернуллі називається схема проведення експериментів:
а) з підкиданням монети; б) з підкиданням грального кубика;
в) незалежних один від одного; г) однакових і незалежних скінченну кількість раз; д) інша відповідь.
Г.
37 Ймовірність того, що деяка подія в схемі Бернуллі з  випробувань відбудеться
випробувань відбудеться  раз дорівнює (
раз дорівнює ( – ймовірність цієї події в кожному випробуванні):
– ймовірність цієї події в кожному випробуванні):
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
38 Найбільш ймовірною кількістю успіхів в схемі Бернуллі з  випробувань та ймовірністю успіху в кожному з них
випробувань та ймовірністю успіху в кожному з них  є:
є:
а)  ; б)
; б) 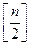 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
39 При великій кількості випробувань за схемою Бернуллі та малоймовірному успіху в кожному випробуванні ймовірність того, що успіх наступить  раз, може бути наближено обчислена за формулою (
раз, може бути наближено обчислена за формулою ( – кількість випробувань,
– кількість випробувань,  – ймовірність успіху в кожному з них):
– ймовірність успіху в кожному з них):
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
40 Функцією розподілу випадкової величини  є функція:
є функція:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
41 Які з рівностей є правильними ( - функція розподілу випадкової величини
- функція розподілу випадкової величини  )?
)?
1) 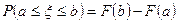 ; 2)
; 2)  ;
;
3)  ;
;
4) 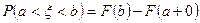 .
.
а) 1 і 3; б) 2 і 4; в) 3 і 4; г) 2 і 3; д) інша відповідь.
Б.
42 Функція розподілу випадкової величини є:
а) неперервною зростаючою функцією; б) неспадною неперервною справа функцією;
в) неспадною неперервною зліва функцією; г) спадною неперервною функцією; д) інша відповідь.
В.
43 Щільність розподілу випадкової величини - це функція  , для якої (
, для якої ( – функція розподілу):
– функція розподілу):
а)  ; б)
; б) 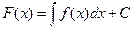 ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
44 Основними властивостями щільності розподілу  є:
є:
а)  ,
,  ; б)
; б)  ,
,  ;
;
в)  ,
, 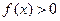 ; г)
; г)  ,
,  ; д) інша відповідь.
; д) інша відповідь.
А.
45 Математичним сподіванням дискретної випадкової величини з розподілом  є:
є:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Б.
46 Які з рівностей для математичного сподівання є неправильними ( - випадкові величини,
- випадкові величини, 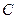 - постійна)?
- постійна)?
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
а) тільки 5; б) 3 і 4; в) 3 і 5; г) 1, 2 і 4; д) інша відповідь.
В.
47 Чи правильна рівність  ?
?
а) правильна; б) неправильна; в) правильна, якщо  і
і  однаково розподілені.;
однаково розподілені.;
г) правильна, якщо  і
і  незалежні; д) інша відповідь.
незалежні; д) інша відповідь.
Г.
48 Математичне сподівання неперервної випадкової величини з щільністю розподілу  дорівнює:
дорівнює:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
А.
49 Математичне сподівання випадкової величини задає:
а) її найбільш ймовірне значення; б) її середнє значення;
в) її найменш ймовірне значення; г) значення, якого потрібно сподіватись; д) інша відповідь.
Б.
50 Дисперсією випадкової величини  є:
є:
а)  ; б)
; б)  ; в)
; в) 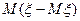 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
51 Дисперсія випадкової величини характеризує:
а) її відхилення від початку координат; б) її відхилення від середнього значення;
в) квадрат відхилення середнього значення випадкової величини від початку координат;
г) середнє значення різниці випадкової величини та її середнього значення; д) інша відповідь.
Б.
52 Які з рівностей для дисперсії є неправильними ( - випадкові величини,
- випадкові величини, 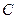 - стала)?
- стала)?
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4) 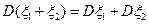 ; 5)
; 5) 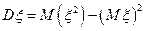 .
.
а) 1, 3 і 4; б) тільки 3; в) 3 і 4; г) 2 і 5; д) інша відповідь.
В.
53 Середньоквадратичне відхилення випадкової величини є:
а) квадратним коренем з дисперсії цієї величини;
б) середнім значенням квадрата цієї величини;
в) відхиленням середнього значення квадрата випадкової величини від її середнього значення;
г) квадратом середнього значення цієї величини; д) інша відповідь.
А.
54 Випадкова величини  має біноміальний розподіл з параметрами
має біноміальний розподіл з параметрами  і
і  . Які із рівностей є абсолютно правильними?
. Які із рівностей є абсолютно правильними?
1) 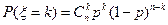 , при
, при  ;
;
2)  ; 3)
; 3) 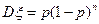 .
.
а) тільки 1; б) тільки 2; в) тільки 3; г) тільки 1 і 2; д) інша відповідь.
Г.
55 Випадкова величини  має розподіл Пуассона з параметром
має розподіл Пуассона з параметром  . Які із рівностей є абсолютно правильними?
. Які із рівностей є абсолютно правильними?
1)  , при
, при  ; 2)
; 2)  ; 3)
; 3)  .
.
а) тільки 1 і 2; б) тільки 1 і 3; в) тільки 2 і 3; г) всі; д) інша відповідь.
А.
56 Випадкова величини  має рівномірний розподіл на відрізку
має рівномірний розподіл на відрізку 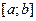 . Які із тверджень є абсолютно правильними?
. Які із тверджень є абсолютно правильними?
1) Її щільність розподілу є кусково сталою; 2) 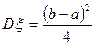 ; 3)
; 3) 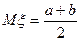 .
.
а) всі; б) тільки 1 і 2; в) тільки 1 і 3; г) тільки 3; д) інша відповідь.
В.
57 Випадкова величини  має нормальний розподіл з параметрами
має нормальний розподіл з параметрами  і
і  . Які із тверджень є абсолютно правильним?
. Які із тверджень є абсолютно правильним?
1)  ,
,  ; 2)
; 2)  ; 3)
; 3) 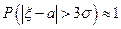 .
.
а) тільки 1 і 2; б) тільки 1 і 3; в) тільки 2 і 3; г) 1, 2 і 3; д) інша відповідь.
А.
58 Випадкова величина  має нормальний розподіл з параметрами
має нормальний розподіл з параметрами  і
і  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1) Щільність розподілу  має вигляд
має вигляд  ;
;
2) щільність розподілу  має вигляд
має вигляд 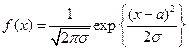 ;
;
3) 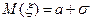 ,
,  ; 4)
; 4)  ,
,  .
.
а) тільки 1; б) тільки 2 і 4; в) тільки 2 і 3; г) тільки 1 і 4; д) інша відповідь.
Г.
59 Які із тверджень правильні для функції Лапласа  ?
?
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 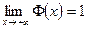 ; 5)
; 5)  .
.
а) 3 і 4; б) 1 і 5; в) 2 і 5; г) 1 і 4; д) інша відповідь.
Б.
60 Функція Лапласа має вид:
а)  ; б)
; б) 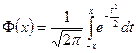 ;
;
в) 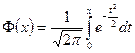 ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
В.
61 Випадкова величина  має показниковий розподіл з параметром
має показниковий розподіл з параметром  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1) Щільність розподілу  має вигляд
має вигляд 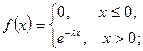
2) щільність розподілу  має вигляд
має вигляд 
3)  ; 4)
; 4)  .
.
а) 2 і 3; б) 1 і 3; в) 2 і 4; г) 1 і 4; д) інша відповідь.
А.
62 Встановити відповідність між щільностями і розподілами.
1)  1) нормальний;
1) нормальний;
2)  2) показниковий;
2) показниковий;
3)  ; 3) рівномірний.
; 3) рівномірний.
а) 1-3, 2-1, 3-2; б) 1-3, 2-2, 3-1; в) 1-1, 2-2, 3-3; г) 1-2, 2-3, 3-1; д) інша відповідь.
Б.
63 Нехай  – коефіцієнт кореляції випадкових величин
– коефіцієнт кореляції випадкових величин  і
і  . Які із тверджень є правильними?
. Які із тверджень є правильними?
1)  , якщо випадкові величини незалежні;
, якщо випадкові величини незалежні;
2) якщо  , то випадкові величини незалежні;
, то випадкові величини незалежні;
3)  тоді і тільки тоді, коли випадкові величини лінійно залежні.
тоді і тільки тоді, коли випадкові величини лінійно залежні.
а) тільки 3; б) тільки 1 і 3; в) тільки 2 і 3; г) тільки 1 і 2; д) інша відповідь.
Б.
64 Коефіцієнтом кореляції двох випадкових величин  і
і  є число рівне:
є число рівне:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д) інша відповідь.
; д) інша відповідь.
Г.
65 Які із наведених значень є параметрами нормального розподілу на площині (двовимірного нормально розподіленого випадкового вектора)?
1) Математичні сподівання кожного з елементів вектора;
2) медіани кожного з елементів вектора;
3) математичне сподівання добутку елементів вектора;
4) коефіцієнт кореляції елементів вектора;
5) коваріація елементів вектора;
6) дисперсії елементів вектора;
7) сума дисперсій елементів вектора.
а) тільки 1, 4 і 7; б) тільки 2, 5 і 4; в) тільки 1, 4 і 6; г) тільки 2, 4 і 6; д) інша відповідь.
В.
66 Згідно із законом великих чисел правильними є такі твердження:
1) Малоймовірно, що середнє арифметичне відхилень випадкових величин від своїх математичних сподівань значно відрізняється від 0, при великій кількості незалежних випадкових величин.
2) Сума великої кількості випадкових величин має приблизно нульове математичне сподівання та одиничну дисперсію.
3) Відносна частота успіху в схемі Бернуллі мало відрізняється від ймовірності успіху в кожному з випробувань, при великій кількості випробувань.
а) тільки 1; б) тільки 2; в) тільки 3; г) тільки 1 і 2; д) інша відповідь.
Д.
67 Нехай  – послідовність незалежних однаково розподілених випадкових величин з математичним сподіванням
– послідовність незалежних однаково розподілених випадкових величин з математичним сподіванням  і дисперсією
і дисперсією  . Які з тверджень є правильними?
. Які з тверджень є правильними?
1)  має стандартний нормальний розподіл;
має стандартний нормальний розподіл;
2)  ;
;
3)  при великих
при великих  має приблизно нормальний розподіл з середнім
має приблизно нормальний розподіл з середнім  і дисперсією
і дисперсією  .
.
4) 
а) тільки 1 і 2; б) тільки 2 і 3; в) тільки 3 і 4; г) тільки 2, 3 і 4; д) інша відповідь.
Б.
68 Нехай  – характеристична функція випадкової величини
– характеристична функція випадкової величини  . В яких із тверджень допущені помилки?
. В яких із тверджень допущені помилки?
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  .
.
а) тільки в 1 і 2; б) тільки в 2 і 3; в) тільки в 3 і 4; г) тільки в 1 і 4; д) інша відповідь.
В.
69 Впорядкуйте шкали вимірювань від найпростішої до найбільш багатої.
1) шкала найменувань; 2) шкала порядку; 3) шкала відношень; 4) шкала інтервалів.
а) 1, 2, 3, 4; б) 2, 1, 4, 3; в) 2, 1, 3, 4; г) 1, 2, 4, 3; д) інша відповідь.
Г.
70 Точкова оцінка  параметра
параметра  розподілу генеральної сукупності називається незміщеною конзистентною (слушною) та ефективною, якщо виконуються такі з наведених вимог:
розподілу генеральної сукупності називається незміщеною конзистентною (слушною) та ефективною, якщо виконуються такі з наведених вимог:
1)  ; 2)
; 2)  , при
, при 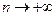 ;
;
3)  , при
, при 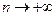 для всіх
для всіх 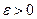 ;
;
4) 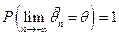 ;
;
5)  є мінімальною серед дисперсій інших оцінок параметра
є мінімальною серед дисперсій інших оцінок параметра  ;
;
6)  є мінімальною серед дисперсій інших незміщених оцінок параметра
є мінімальною серед дисперсій інших незміщених оцінок параметра  .
.
а) 1, 2 і 3 відповідно; б) 1, 3 і 6 відповідно; в) 2, 4 і 6 відповідно; г) 2, 4 і 5 відповідно; д) інша відповідь.
Б.
71 Які з оцінок є оцінками математичного сподівання?
1)  ; 2) медіана; 3)
; 2) медіана; 3)  ; 4) мода.
; 4) мода.
а) тільки 1, 3 і 4; б) тільки 2, 3 і 4; в) тільки 1, 2 і 3; г) тільки 1; д) інша відповідь.
В.
72 Які з оцінок не є оцінками дисперсії генеральної сукупності?
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
Поиск по сайту: