Формула Бернуллі

Часто при дослідженні деякої випадкової події А організовують експеримент за такою схемою:

1) проводять п послідовних незалежних випробувань, в кожному з яких може відбутися подія А;

2) ймовірність події А в кожному випробуванні є величина стала Р(А)=р, тоді Р()=q, відомо, що Р(А)+ Р()=1 Þ p+q=1;

3) ставиться питання, яка ймовірність того, що при цих п незалежних випробуваннях, подія А настане к разів (0≤ к ≤ п). Аналітично це виглядає так: ? або –?

Експеримент організований за такою схемою називають схемою повторних незалежних випробувань Бернуллі.

Ймовірність того, що подія А настане к разів в п випробуваннях знаходиться за формулою Бернуллі:

, де (7)

Число k₀, при якому ймовірність найбільша, називається найімовірнішим числом настання події А. Знайти його можна за формулою – ціла частина числа . Якщо виявиться, що число – ціле, то к₀ -1 також буде найімовірнішим числом настання події А.

Задача. 18. Що більш ймовірно: виграти у гравця у шахи (рівного собі за силою гри) чотири партії з восьми, чи три партії з п’яти?

Розв’язання. За умовою , .

Скориставшись формулою (7), одержимо:

,

.

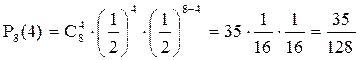Відповідь: Оскільки > , то більш ймовірно виграти три партії з п’яти, чим чотири з восьми.

Поиск по сайту: