АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Згрупований розподіл накопиченої частоти

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  3. Біноміальний закон розподілу
  4. Випадкові величини та їх розподіл
  5. Випадкові змінні х та у стохастично залежні, якщо зміна однієї з них викликає зміну розподілу другої (умовний розподіл однієї з них залежить від значень другої).
  6. Властивості емпіричної функції розподілу
  7. Властивості функції розподілу
  8. Геометричний закон розподілу
  9. Геометричний закон розподілу 1 страница
  10. Геометричний закон розподілу 2 страница
  11. Геометричний закон розподілу 3 страница
  12. Геометричний закон розподілу 4 страница

У прикладах 1,2 складені дискретна та інтервальна таблиці частот вказують на зв’язок між значеннями досліджуваної ознаки і відповідними частотами. У математичній статистиці такий зв’язок називають розподілом частоти.

Часто з розподілу частоти необхідно мати розподіл (кумулятивної) накопиченої частоти. Його одержують послідовним додаванням частот окремих значень варіант, або частот інтервалів починаючи з першого і закінчуючи останнім.

Позначають накопичену частоту F. Насамперед складемо дискретний варіаційний ряд з накопиченими частотами. Скористаємося для цього прикладом 1.

аі        
ki        
Fi        


Розподіл накопиченої частоти дозволяє відповісти на запитання: „Скільки існує учнів, що отримали оцінку менше ніж „4”?”

Аналогічно отримаємо розподіл накопиченої відносної частоти

аі        
ki        
0,05 0,48 0,73  

 

 

Розподіл відносної накопиченої частоти дозволяє відповісти на запитання: „Який відсоток учнів, що отримали оцінку менше ніж „4”?”

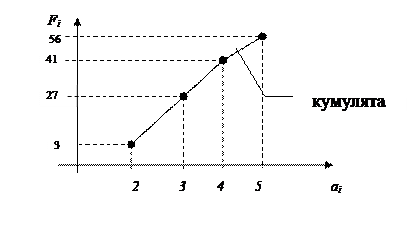
Для графічного зображення розподілу накопиченої частоти будують кумуляту або огиву.

 

Означення. Кумулята – ламана лінія, відрізки якої сполучають точки, абсцисами яких є значення варіант, а ординатами відповідні їх накопичені частоти. Якщо координати точок переставити місцями, то отримаємо огиву.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)