АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Геометричний закон розподілу

Читайте также:
  1. B) Наличное бытие закона
  2. II закон Кирхгофа
  3. II. Законодательные акты Украины
  4. II. Законодательство об охране труда
  5. II.3. Закон как категория публичного права
  6. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  7. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  8. IX.3.Закономерности развития науки.
  9. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  10. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  11. А) Закон диалектического синтеза
  12. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.

Нехай проводяться незалежні випробування, в кожному з яких ймовірність появи події А рівна р (0 < p < 1), а не появи q = 1- p. Випробування закінчуються, як тільки відбувається подія А. Таким чином, якщо подія А відбулась в k -му випробуванні, то попередніх k-1 випробування Х є: х 1=1, х 2=2, …

Нехай в перших k-1 випробуваннях подія А не відбулася, а в k -му випробуванні з’явилась. Тоді ймовірність рівна

(6)

Покладаючи k=1,2, … у формулі (6), отримаємо геометричну прогресію з першим членом Р і знаменником q (0<q<1): p,qp,q2p, … qk- 1 p, … тому розподіл називається геометричним.

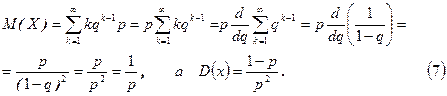
Приклад 3. Проводяться багаторазові випробування елементу на надійність до тих пір, поки він не відмовить в роботі. Ймовірність відмови елементу в кожному випробуванні рівна 0,1. Знайти числові характеристики випадкової величини Х – числа випробувань, які треба провести.

Рішення. По умові р = 0,1. Тому

.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)