Дисперсія і середнє квадратичне відхилення

Для характеристики випадкової величини недостатньо знати лише її математичне сподівання, так як одному і тому ж математичному сподіванню може відповідати нескінченна множина випадкових величин з різними законами розподілу.

Значення випадкових величин завжди коливається біля середнього значення. Це явище називається розсіюванням величини біля її середнього значення.

Основними характеристиками розсіювання випадкової величини є середнє квадратичне відхилення.

Означення. Дисперсією D[X] випадкової величини X називається математичне сподівання квадрату відхилення цієї величини від її математичного сподівання:

.

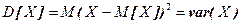Для дискретної випадкової величини дисперсія виражається сумою:

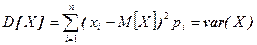(1)

а неперервної – інтегралом:

(2)

Дисперсія випадкової величини є зручною характеристикою розсіювання, але вона має той недолік, що має розмірність квадрату випадкової величини.

Для більшої зручності вводиться характеристика, що має розмірність випадкової величини, а саме – корінь квадратний з дисперсії:

, (3)

і її називають середнім квадратичним відхиленням, або стандартом.

Зауваження. Якщо брати математичне сподівання відхилення випадкової величини від її математичного сподівання, то отримуємо завжди:

.

Цей результат є цілком природним, він показує, що випадкова величина відхиляється від свого математичного сподівання як вправо, так і вліво, а тому додатні та від’ємні значення знищуються і він ніякої характеристики розсіювання не дає.

Найпростіші властивості дисперсії:

Властивість 1. Дисперсія будь-якої випадкової величини невід’ємна.

Доведення безпосередньо випливає з означення дисперсії, так як .

Властивість 2. Дисперсія постійної величини рівна нулю: D(C)=0.

Доведення. Дійсно

Властивість 3. Дисперсія добутку сталої величини на випадкову величину рівна добутку квадрату постійної величини на дисперсію випадкової величини:

D(CX)=C²D(X).

Властивість 4. Дисперсія випадкової величини дорівнює різниці між математичним сподіванням квадрату цієї величини і квадратом її математичного сподівання:

D(X)=M(X)²-M²D(X) (4)

Доведення. Дійсно

M(X-M(X))²=M(X²-2M(X)X+M²(X))=M(X²)-2M(X)M(X)+M(M²(X))=

=M(X²)-2M²(X)+M²(X)=M(X²)-M²(X).

Властивість 5. Дисперсія об’єднання двох незалежних випадкових величин дорівнює сумі їх дисперсії:

D(XÈY)=D(X)+D(Y) (5)

Доведення. Дійсно D(XÈY)=M(XÈY)²-M²(XÈY)=M(X²È2XYÈY²)-

-(M(X)+M(Y))²=M(X²)+2M(X)M(Y)+M(Y²)+M(Y²)-M²(X)-2M(X)M(Y)-

-M²(Y)=(M(X²)-M²(X))+M(Y²)-M²(Y)=D(X)+D(Y).

Наслідок 1. Дисперсія різниці незалежних випадкових величин рівна сумі їх дисперсій.

Наслідок 2. Дисперсія суми скінченного числа незалежних випадкових величин рівна сумі їх дисперсій.

Наведемо теореми про математичне сподівання і дисперсію деяких дискретних випадкових величин.

Теорема 1. Якщо Х₁ Х₂…Х_n – однаково розподілені випадкові величини, математичні сподівання кожної з яких рівне а, то математичне сподівання їх об’єднання рівне n a, а математичне сподівання середньої арифметичної рівне а.

Теорема 2. Якщо Х ₁ Х₂…Х_n – однаково розподілені випадкові величини, дисперсія кожної з яких рівна s²_х, то дисперсія їх об’єднання рівна n s²_х, а дисперсія середньої арифметичної рівна .

Поиск по сайту: