АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Закони розподілу дискретних випадкових величин

Читайте также:
  1. IV. Относительные величины, динамические ряды
  2. V. Вариационные ряды, средние величины, вариабельность признака
  3. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  4. XIV. 7. Вимірювання електрорушійних сил. Застосування методу вимірювання ЕРС для визначення різних фізико – хімічних величин
  5. А. Средняя квадратическая погрешность функции измеренных величин.
  6. Абсолютные величины
  7. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ВЕЛИЧИНЫ
  8. АКУСТИЧНІ ВЕЛИЧИНИ
  9. Алгебра випадкових подій
  10. Алгоритм изменения дозы НФГ в зависимости от относительной величины АЧТВ (по отношению к контрольной величине конкретной лаборатории)
  11. Алгоритм оценки погрешностей прямых измерений физических величин
  12. Анализ влияния эффективности использования материальных ресурсов на величину материальных затрат

Задають дискретні випадкові величини за допомогою закону розподілу, коли задаються ймовірності їх можливих випадкових значень (див. § 1). Залежно від того, за якою формулою будуть обчислюватися ймовірності Рі, ці закони будуть мати свою назву.

Біноміальний розподіл – це закон розподілу випадкових величин, заданий таблицею, у якій ймовірності Рі обчислюються за формулою Бернуллі:

(див. лк.23 §1).

Х 0 1 … і … n
р qn C1np qn-1 … C1npi qn-1 … pn

п

де p, n, q = 1-p, називаються араметрами розподілу.

Математичне сподівання і дисперсія випадкової величини, що має біноміальний розподіл відповідно рівні:

.

Приклад 1. Митний пост дає статистичну оцінку того, що 20% усіх осіб, що повертаються з-за кордону, не декларують весь товар, який підлягає оподаткуванню. Якщо випадково відібрати 5 осіб, то записати закон розподілу випадкової величини Х – кількість осіб, що не декларують весь товар, привезений з-за кордону та знайти математичне сподівання і середнє квадратичне відхилення.

Рішення. В даному випадку р=0,2; q=0,8; n=5.

Тоді

Х            
Р 0,32768 0,4096 0,2048 0,0512 0,0064 0,0032

Пуассонівський закон розподілу – це закон розподілу випадкової величини, заданий таблицею, у якій ймовірність обчислюється за формулою Пуассона 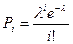(див. лк.23, §3).

Х 0 1 … і … n
Р е-l lе-l … …

 

де n®¥, l=n p.

Типовими прикладами випадкової величини, що має розподіл Пуассона, є: число викликів на АТС за деякий час t; число відновлень складної апаратури за час t, якщо відомо, що відновлення незалежні один від одного і в середньому на одиницю часу випадає l відновлень і т.п.

Розподіл Пуассона залежить від одного параметру l, який є математичним сподіванням випадкової величини Х:

.

Дисперсія буде:

звідси: .

Приклад 2. Завод відправив споживачу 5000 якісних виробів. Ймовірність пошкодження виробу в дорозі рівна 0,0002. Записати закон розподілу чотирьох пошкоджених виробів та зобразити його графічно.

Рішення. З умови: l=np=5000× 0,0002=1 тому

P4(0)=0,36788,

P4(1)=0,36788, P4(2)=0,0,18394, P4(3)=0,06131, P4(4)=0,01533.

 

Х          
Р 0,36788 0,36788 0,18394 0,06131 0,01533

 

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)