Формула повної ймовірності. Формула Байеса

Нехай А – деяка подія, яка може відбутись або не відбутись одночасно з однією з подій Н₁, Н₂,...Н_n, що утворюють повну групу несумісних подій 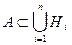. Події Н₁, Н₂,...Н_n називають гіпотезами. Ймовірності всіх гіпотез відомі Р(Н_і) (і= ), а також відомі умовні ймовірності події А при кожній гіпотезі, тобто дано: .

Тоді ймовірність події А визначається теоремою.

Теорема 1. (формула повної ймовірності). Ймовірність події А, що може відбутись разом з однією з гіпотез Н₁, Н₂,...Н_n, дорівнює сумі добутків ймовірності кожної з гіпотез на відповідну умовну ймовірність події А:

. (1)

Доведення. Так як гіпотези Н₁, Н₂,...Н_n утворюють повну групу подій, то подію А можна записати як: , а оскільки несумісні, то:

.

Теорема доведена.

До цих пір розглядалася ймовірність події до випробовування, тобто в комплексі умов не був присутній результат проведеного випробовування.

Тому поставимо тепер наступну задачу. Є повна група несумісних гіпотез Н₁, Н₂,...Н_n. Відомі ймовірності кожної з гіпотез . Проводиться випробування і в його результаті відбувається подія А, ймовірності якої по кожній гіпотезі відомі, тобто .

Виникає питання, які ймовірності мають гіпотези H_i в зв’язку з появою події А? Тобто були відомі ймовірності апріорні (від латинського a priori – до випробовування). Якщо ж подія А відбулася, то чи можна переоцінити ймовірності кожної з гіпотез ? Ці нові ймовірності будуть вже апостеріорними ймовірностями гіпотез (від латинського a posteriori – після випробовування).

Відповідь на це питання дає теорема Байеса.

Теорема 2. Ймовірність гіпотези після випробовування рівна добутку ймовірності гіпотези до випробовування на відповідну їй умовну ймовірність події, яка відбулася в результаті випробовування, поділеній на повну ймовірність цієї події:

. (2)

Доведення. З аксіоми множення ймовірностей випливає:

Звідки

Теорема доведена.

Приклад 1. До магазину надходять вироби з двох заводів, причому з першого 150 штук, а з другого 250. Перший завод випускає в середньому 0.5% бракованої продукції, другий – 0.2%. Яка ймовірність купити в магазині бракований виріб?

Рішення. Нехай подія А є купівля бракованого виробу, гіпотеза Н₁ – виріб, випущений першим заводом, гіпотеза Н₂ – другим заводом. Тоді

По формулі повної ймовірності:

Приклад 2. Спеціалізована лікарня приймає в середньому 50% хворих, що мають захворювання Н₁, 30% - захворювання Н₂ і 20% - Н₃. Статистика свідчить, що ймовірність повного виліковування хвороби Н₁ дорівнює 0.9, для хвороби Н₂ – 0.7 і для хвороби Н₃ – 0.8. Яка ймовірність того, що пацієнт, виписаний з лікарні цілком здоровим (подія А), був хворий на хворобу Н₂?

Рішення.

Згідно формули Байеса

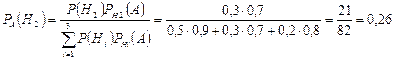
Поиск по сайту: