Законом великих чисел і центральною граничною теоремою

При доведенні теорем, що відносяться до групи “ закону великих чисел”, використаємо нерівність Чебишева.

§1. Нерівність Чебишева

Нехай Х – випадкова величина з математичним сподіванням . Виберемо деяке число і розглянемо подію

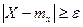(1)

Геометричний зміст цієї події полягає в тому, що значення випадкової величини Х попаде в область на числовій осі, що одержується виділенням з усієї осі інтервалу . Із збільшенням ця область зменшується, тобто ймовірність попадання в неї зменшується. Нерівність Чебишева якраз і встановлює для цієї ймовірності дуже просту оцінку.

Нерівність Чебишева. Ймовірність того, що відхилення випадкової величини від її математичного сподівання по абсолютній величині не менше довільного додатнього числа , обмежена зверху величиною :

. (2)

Доведення. Доведення проведемо для дискретної випадкової величини Х з рядом розподілу

			...
Рk	Р1	Р2	...	Рn

Тоді дисперсія величини є .

Оскільки всі доданки невід’ємні, то відкинемо ті, у яких , тим самим одержимо:

, (3)

де запис під знаком суми означає, що сумування поширюється лише на ті значення і, для яких 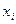відхиляється від 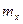на величину, не меншу, ніж .

Замінимо під знаком суми (3) вирази , то від такої заміни сума лише зменшиться, тобто:

(4)

В свою чергу під знаком суми в (4) маємо ймовірність того, що випадкова величина набирає значення 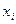, які відхиляються від математичного сподівання 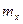на величину, не меншу ніж . Значить,

або ,

що й потрібно було довести.

Зауваження. Нерівність Чебищева практично має обмежене значення, оскільки часто дає грубу оцінку. Наприклад, , тоді

.

Але й без оцінки відомо, що ймовірність 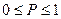. З іншої сторони, якщо, наприклад, , то

.

А це вже непогана оцінка ймовірності, тобто нерівність Чебишева корисна лише при відносно великих .

Теоретичне ж значення нерівності Чебишева дуже велике. Використаємо цю нерівність для доведення теореми Чебишева.

§2. Теорема Чебишева

Означення. Послідовність випадкових величин Х₁, Х₂,...Х_n,... збігається по ймовірності до величини а, якщо для довільного

.

Теорема Чебишева. Якщо Х₁, Х₂,...Х_n,... попарно незалежні випадкові величини, що мають рівномірно обмежені дисперсії , то для будь-якого малого числа , ймовірність нерівності

буде як завгодно близька до одиниці, якщо число випадкових величин достатньо велике, тобто

.

Отже, теорема Чебишева стверджує, що коли розглянути досить велике число незалежних випадкових величин, що мають обмежені дисперсії, то майже достовірною є подія, що відхилення середнього арифметичного випадкових величин від їх математичного сподівання буде по абсолютній величині як завгодно малим числом.

Доведення. Розглянемо випадкову величину і знайдемо її числові характеристики:

(при умові ).

Застосуємо нерівність Чебишева до випадкової величини :

.

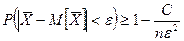Яке б не було мале , то при , величина , тобто

.

Теорема Чебишева має практичне застосування в теорії похибок, коли за істинне значення деякої величини беруть середнє арифметичне даних, отриманих в експериментах, що проводяться в однакових умовах. В математичній статистиці по теоремі Чебишева побудований вибірковий метод, суть якого полягає в тому, що про поведінку всієї сукупності можна судити за даними невеликої випадкової вибірки.

Приклад 1. Ймовірність, що холодильник витримає гарантійний термін роботи, дорівнює 0.8 для всіх 100 холодильників, які обслуговує гарантійна майстерня. Оцінити ймовірність, що число холодильників, які витримають гарантійний термін роботи, буде в межах [75;85].

Рішення. Випадкова величина Х – число холодильників, що витримають гарантійний термін роботи, розподілена за біноміальним законом, тому , , .

Використаємо нерівність Чебишева:

.

§3. Теорема Бернуллі

Частковим випадком теореми Чебишева є теорема Бернуллі. Ця теорема вважається початком теорії ймовірності як науки.

Теорема Бернуллі. Нехай у кожному із n незалежних випробувань ймовірність появи події А є постійно р. Тоді

,

де - відносна частота події А.

Доведення. Нехай випадкова величина Х₁ – число появи події А в першому випробуванні, Х₂ – число появи події А в другому випробуванні і т.д. Тоді кожна з величин Х_і має розподіл:

де q=1-p.

Тоді: , ,

.

Застосуємо теорему Чебишева

для будь-якого числа .

§4. Центральна гранична теорема Ляпунова

Розглянуті в попередніх параграфах теореми є різними формами закону великих чисел і встановлюють факти збіжності по ймовірності деяких випадкових величин до їх постійних характеристик. При цьому ні в одній з них ми не мали справу з законами розподілу випадкових величин.

В цьому параграфі ми розглянемо питання, зв’язане з знаходженням граничного закону розподілу об’єднання

,

коли число складових необмежено зростає. Центральна гранична теорема теорії ймовірності (теорема Ляпунова) встановлює умови, при яких вказаний граничний закон є нормальним.

Сформулюємо просту форму центральної граничної теореми, коли випадкові величини Х₁, Х₂,...Х_n,... взаємно незалежні.

Теорема. Якщо випадкова величина є об’єднанням великого числа взаємно незалежних величин, вплив кожної з яких на всю суму є дуже незначним, то Y має розподіл, близький до нормального.

Ця теорема дає одну з можливих відповідей на питання, чому нормально розподілені випадкові величини часто зустрічаються на практиці.

Приклад 1. Кожна зі 100 незалежних випадкових величин розподілена за показниковим законом розподілу з параметром . Побудувати наближений закон розподілу випадкової величини .

Рішення. Оскільки значення густини показникового закону розподілу для x>0 і - число мале порівняно зі всією сумою, то його вплив на Y незначний. Тоді по теоремі Ляпунова Y буде розподілена за законом, близьким до нормального.

За умовою ; , а тому

, .

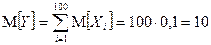Густина розподілу має вигляд: , .

Приклад 2. Кожна з 24 незалежних випадкових величин розподілена за рівномірним законом на інтервалі (0,1). Записати наближений вигляд для густини об’єднання цих випадкових величин. Знайти ймовірність того, що сума буде в межах від 6 до 8.

Рішення. За теоремою Ляпунова випадкова величина буде мати розподіл близький до нормального. Порахуємо , , , .

Отже, густина розподілу , тому:

.

Поиск по сайту: