 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нормальний закон розподілу. Серед розподілів неперервних випадкових величин центральне місце займає нормальний (закон Гаусса)
Серед розподілів неперервних випадкових величин центральне місце займає нормальний (закон Гаусса). Він часто застосовується в задачах практики, проявляється в тих випадках, коли випадкова величина Х є результатом дії великого числа факторів, кожний з яких окремо на величину Х впливає мало і не можна виділити, який більше, а який менше.
Основна особливість, що виділяє нормальний закон серед інших, полягає в тому, що він є граничним законом, до якого наближаються інші закони розподілу.
Означення. Нормальним називається розподіл ймовірностей неперервної випадкової величини, якщо її густина розподілу має вигляд:
 (12)
(12)
для довільного значення  і довільних чисел
і довільних чисел 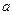 і
і 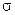 .
.
Числа 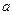 і
і 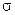 називають параметрами розподілу і мають певний ймовірнісний зміст, який розглянемо нижче.
називають параметрами розподілу і мають певний ймовірнісний зміст, який розглянемо нижче.
Графіком функції (12) є крива, яку в літературі називають кривою Гаусса, або нормальною кривою.
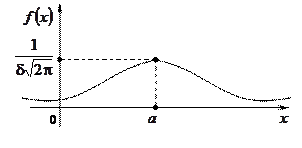 |
Якщо у формулі (12) покласти  , отримуємо нормовану функцію Гаусса, яка нам уже траплялася в теоремах Муавра-Лапласа (див. лк.23, §3) під назвою функції Лапласа.
, отримуємо нормовану функцію Гаусса, яка нам уже траплялася в теоремах Муавра-Лапласа (див. лк.23, §3) під назвою функції Лапласа.
Бачимо, що нормальний розподіл визначається двома параметрами: 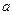 і
і 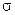 . Досить знати ці параметри, щоб задати нормальний закон розподілу. Доведемо, що ймовірнісний зміст цих параметрів наступний:
. Досить знати ці параметри, щоб задати нормальний закон розподілу. Доведемо, що ймовірнісний зміст цих параметрів наступний: 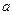 - математичне сподівання, а
- математичне сподівання, а 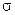 - середнє квадратичне відхилення. Дійсно:
- середнє квадратичне відхилення. Дійсно:
а)
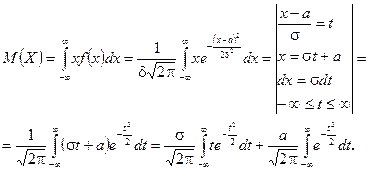
Перший доданок  , бо функція непарна, а інтегрування ведеться в межах, симетричних відносно початку координат; другий доданок
, бо функція непарна, а інтегрування ведеться в межах, симетричних відносно початку координат; другий доданок  - інтеграл Пуассона, отже:
- інтеграл Пуассона, отже:
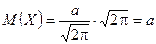 . (13)
. (13)
б)
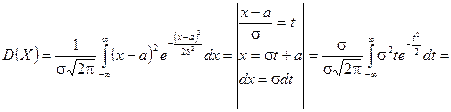
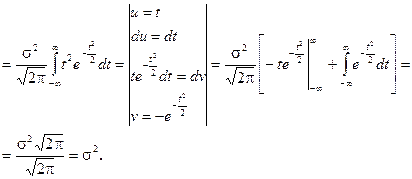
 . (14)
. (14)
Відмітимо деякі властивості нормальної кривої:
а) крива симетрична відносно прямої 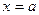 і
і 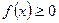 ;
;
б) крива має один максимум при 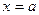 , бо
, бо  при
при 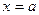 ,
,  при
при 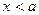 і
і 
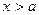 , при
, при 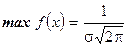 ;
;
в) крива асимптотично наближається до осі 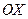 , бо
, бо 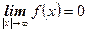 ;
;
г) зміна математичного сподівання 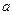 при
при 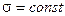 призводить до зміщення кривої Гаусса вздовж осі
призводить до зміщення кривої Гаусса вздовж осі 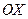 .
.
 При зміні середнього квадратичного відхилення
При зміні середнього квадратичного відхилення 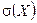 і
і 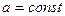 крива розподілу міняє свій вигляд (див рис.1), де крива І відповідає
крива розподілу міняє свій вигляд (див рис.1), де крива І відповідає 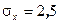 , крива ІІ -
, крива ІІ - 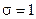 , а для кривої ІІІ -
, а для кривої ІІІ - 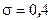 ,
, 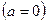 .
.
Поряд з диференціальною функцією розподілу (12) нормального закону розподілу розглянемо й інтегральну функцію. Згідно з означенням, маємо:
 .
.
Перший інтеграл відомий в літературі як інтеграл Пуассона і його значення дорівнює 0,5. Тоді у другому робиться заміна  :
:
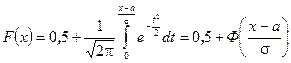 . (15)
. (15)
Як наслідок з формули (15) отримаємо ймовірність попадання випадкової величини, розподіленої за нормальним законом, в інтервал 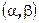 :
:

 (16)
(16)
Легко встановити і відхилення випадкової величини від її математичного сподівання 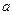 на наперед задану величину
на наперед задану величину  :
:
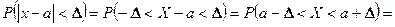
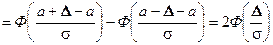 . (17)
. (17)
З останньої формули (17) легко встановити правило трьох сигм, а саме, покладемо  .
.
 .
.
Якщо 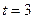 , тобто
, тобто 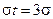 , то
, то
 (18)
(18)
В цьому полягає сутність правила трьох сигм: якщо випадкова величина розподілена нормально, то абсолютна величина її відхилення від математичного сподівання не перевищує потроєного середнього квадратичного відхилення.
Приклад 1. Похибка радіодальноміра має нормальний закон розподілу з 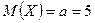 м,
м,  м. Знайти ймовірність того, що виміряне значення дальності буде відхилятися від істинного не більше, ніж на 20 м.
м. Знайти ймовірність того, що виміряне значення дальності буде відхилятися від істинного не більше, ніж на 20 м.
Рішення. Скористаємось формулою (17):
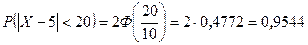 .
.
Поиск по сайту: