АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Гранична теорема Пуассона

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. S-M-N-теорема, приклади її використання
  3. Внешние эффекты (экстерналии). Теорема Коуза.
  4. Внешние эффекты, их виды и последствия. Теорема Коуза
  5. Вопрос 1 теорема сложения вероятностей
  6. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  7. Вопрос. Теорема Котельникова (Найквиста)
  8. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  9. Гранична норма заміщення
  10. Дискретизація сигналу – теорема відліків (Котельникова)
  11. Друга теорема економіки добробуту та її значення

Точність наближених формул Муавра-Лапласа погіршується з наближенням одного з чисел р чи q до нуля. Тому випадок, коли р чи q є малим числом, потребує окремого розгляду. Тобто нас цікавить оцінка для ймовірності числа подій, коли подія рідко відбувається.

Теорема 3. (Пуассона). Нехай 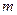фіксоване, а і 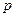міняються, причому так, що величина 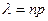є постійною. Тоді

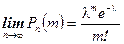
Із граничної теореми Пуассона випливає наближена формула Пуассона при великих і малих р (р<0,1):

,

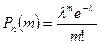де число 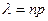називається середнім числом успіхів.

Сукупність значень 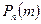називається розподілом Пуассона.

Приклад 3. Із статистичного зведення визначено, що ймовірність захворіти грипом під час епідемії для кожної особи складає 0,08. Яка ймовірність того, що із 100 перевірених осіб хворими виявляться рівно 10 осіб?

Рішення. За умовою n=100, m=10, p=0,08.

Тому

.

Отже,


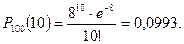
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)