Випадкові величини та їх розподіл

До цих пір ми мали справу з випадковими подіями. Подія є якісною характеристикою випадкового результату випробування. Але цей випадковий результат випробування можна характеризувати і кількісно, тобто вважати, що випадкова величина – це змінна, значення якої залежить від випадку. Якщо намагатися дати цьому означенню більш точного змісту, то потрібно говорити про функцію, значення якої визначаються результатами випробування. Але результати випробування – це точки простору елементарних подій W, тому природно називати випадковою величиною функцію Х=Х(w), визначену на просторі елементарних подій W. Наведемо деякі приклади.

1. Випробування полягає в киданні правильного грального кубика; простір елементарних подій є W.={w₁,w₂,w_3,w_4,w_5,w₆} (w_і – випадання грані в і очок). Нехай Х(w_і)=і, тобто кожному киданню кубика поставимо у відповідність число очок, що випало при цьому киданні.

2. Проводиться серія з n послідовних незалежних випробувань Бернуллі. Кожна елементарна подія – це деяка послідовність успіхів і невдач в n випробуваннях. Позначимо через Х(w) число успіхів в елементарній події w; Х(w) може набути будь-якого цілого значення від 0 до n.

3. Випробування полягає в тому, що послідовно підкидається симетрична монета до першого випадання цифри; простір елементарних подій у цьому випадку нескінченний, а саме зліченний: W.={w₁,w₂,...._,w_n,...}, де w₁=ц,w₂ = гц,w₃=ггц, w_n=г...гц (г – випадання герба, ц – випадання цифри). Нехай Х(w_і)=і (тобто Х – це число підкидань монети до першого випадання цифри); можливі значення Х – будь-які натуральні числа.

4. Випробування полягає в тому, що стрілець робить один постріл по мішені. Простір елементарних подій W - множина всіх точок множини мішені. Для кожної точки wÎW позначимо через Х(w) відстань від точки w до центра мішені (тобто Х – відстань від точки, в яку попала куля, до центра мішені); Х – може набирати будь-якого невід’ємного значення.

У наведених прикладах розглянуто ряд випадкових величин – функцій на множині елементарних подій. Але з теоретико-ймовірносної точки зору задання тільки самої функції ще недостатньо для характеристики випадкової величини, треба ще мати змогу відповідати на запитання, зв’язані з ймовірностями значень, що їх набуває функція Х(w). Так, у прикладах 1-3, легко знайти ймовірності набування окремих значень. У першому прикладі 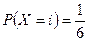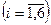. У другому прикладі 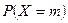обчислюється за формулою Бернуллі; у третьому прикладі, очевидно,

Поиск по сайту: