 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Лекція 3. ПОСЛІДОВНІ НЕЗАЛЕЖНІ ВИПРОБУВАННЯ
§1. Схема Бернуллі
Нехай проводиться серія випробувань, в результаті якої може відбутись подія А з певною ймовірністю. Якщо ймовірність події А в кожному випробуванні не залежить від результатів інших випробувань, то такі випробування називаються незалежними відносно події А.
Поставимо задачу.
Знайти ймовірність того, що в результаті проведення n незалежних випробувань подія А відбудеться рівно m раз, якщо в кожному із цих випробувань дана подія відбувається з постійною ймовірністю 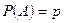
 .
.
Шукану ймовірність позначають 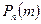 . Наприклад,
. Наприклад,  означає ймовірність того, що при 8-ми випробуваннях подія А відбудеться 4 рази.
означає ймовірність того, що при 8-ми випробуваннях подія А відбудеться 4 рази.
Такі випробування називають послідовними незалежними випробовуваннями Бернуллі. Прикладами можуть бути послідовні підкидання монети (подія А – випадання герба,  ), послідовні підкидання грального кубика (подія А – випадання 5 очок,
), послідовні підкидання грального кубика (подія А – випадання 5 очок,  ).
).
Дану задачу можна розв’язати з допомогою теорем додавання і множення ймовірностей, але це призводить до дуже громіздких обчислень.
Тому виникає необхідність застосування простіших методів розрахунку. Одним з таких методів є формула Бернуллі.
Нехай в однакових умовах проводиться n випробувань, результатом кожного з них подія А може відбутися з ймовірністю 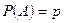 , або ж
, або ж 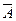 з ймовірністю
з ймовірністю  . Позначимо через
. Позначимо через 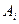
 появу події А в і-му випробуванні. Тоді:
появу події А в і-му випробуванні. Тоді:
 ,
,

Нас цікавить ймовірність того, що подія А при n випробуваннях відбудеться m раз, а в решті n-m випробуваннях відбудеться подія 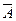 (подія А не відбудеться).
(подія А не відбудеться).
Так як подія А в n випробуваннях може появитись m раз в різних послідовностях або комбінаціях, то число таких комбінацій є  .
.
Наприклад, така сполука (позначимо її подіїю В) є:

коли подія А відбулася m раз підряд, починаючи з першого випробування.
Знайдемо її ймовірність:
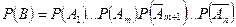
Так як всі комбінації події, аналогічні комбінації В, є подіями
несумісними і нам байдуже, в якій саме послідовності з’явиться подія А та 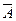 , то, застосовуючи теорему додавання ймовірностей для несумісних подій, отримаємо:
, то, застосовуючи теорему додавання ймовірностей для несумісних подій, отримаємо:
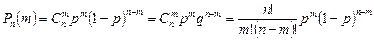 . (1)
. (1)
Формула (1) носить назву формули Бернуллі і має важливе значення в теорії ймовірності, бо вона зв’язана з повторенням випробувань в однакових умовах, тобто з такими умовами, в яких якраз і проявляються закони теорії ймовірності.
Набір чисел 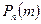
 називається біномним розподілом, а саму формулу (1) називають біномною, оскільки її права частина є загальним членом розкладу бінома Ньютона
називається біномним розподілом, а саму формулу (1) називають біномною, оскільки її права частина є загальним членом розкладу бінома Ньютона  . Зауважимо, що події
. Зауважимо, що події 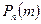
 є попарно несумісні, тому
є попарно несумісні, тому
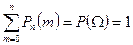
тобто

Приклад 1. Податкова адміністрація виявила, що 40% декларацій про доходи осіб – платників податку – містить принаймі одну похибку. Яка ймовірність того, що з 10 наугад відібраних декларацій, 4 буде з похибкою?
Рішення. Ймовірність, що декларація має похибку  а
а  . Тоді:
. Тоді:

Поиск по сайту: