Багатофакторна регресія

На практиці економічний процес змінюється під впливом багатьох різноманітних факторів, які треба вміти виявити та оцінити. Якщо розглянути приклад з лк 30, то аналіз обсягу продажу на фірмі було б спрощено допускати тільки від витрат на рекламу. На обсяги продажу впливає частина ринку, яку утримує фірма, якість продукції, імідж марки продукції, середня заробітна плата населення у регіонах продажу та інші фактори.

Узагальнена багатофакторна лінійна регресійна модель може бути записана у вигляді:

у = а₀+а₁х₁+а₂х₂+…+а_рх_р+e, (1)

де у – залежна змінна, х₁, х₂,…х_p – незалежні змінні (фактори) а₀, …а_р – параметри моделі, які потрібно оцінити, e - не спостережувана випадкова величина.

Узагальнена регресійна модель – це модель, яка дійсна для всієї генеральної сукупності. Невідомі параметри узагальненої моделі є константами, а випадкова величина – не спостережувана, і можна лише зробити припущення відповідно до закону її розподілу. На відміну від узагальненої регресійної моделі, вибіркова модель будується для певної вибірки; невідомі параметри вибіркової моделі є випадковими величинами, математичне сподівання яких дорівнює параметрам узагальненої моделі.

Відповідна вибіркова лінійна багатофакторна модель має вигляд:

ŷ = b₀+b₁х₁+…+b_рх_р+e, (2)

де ŷ – залежна змінна, х₁…х_р – незалежні змінні, b₀, b₁…b_р – оцінки невідомих параметрів узагальненої моделі, е – випадкова величина (помилка).

Нехай дано ряд спостережень за залежною змінною та за незалежними змінними, або факторами: . На підставі цих спостережень будується лінійна вибіркова багатофакторна модель, а саме – у вигляді (2).

Як і у випадку простої лінійної регресії, знаходять невідомі параметри за методом найменших квадратів, тобто мінімізують суму квадратів відхилень фактичних даних від теоретичних:

тобто .

Звідки отримується нормальна система рівнянь:

(3)

Розв’язуючи систему рівнянь (3) щодо b₀, b₁…b_р одержують рівняння множинної регресії.

Лінійну багатофакторну модель, як і основні проблеми регресійного аналізу, зручно розглядати за допомогою матриць. Для цього введемо матриці:

Тоді систему (2) можна записати у матричній формі

, (4)

а систему (3) можна записати у такому матричному вигляді:

, (5)

або Х^ТХВ =X^TY Якщо обернена матриця Х^ТХ існує (Х^ТХ)^-1, то, помноживши на неї останню рівність, отримаємо:

(Х^ТХ)^-1(Х^ТХ) В = (Х^ТХ)^-1 Х^ТY, або остаточно:

(6)

Рівняння (6) є фундаментальним результатом для визначення невідомих вибіркових параметрів у матричному вигляді.

§2. Нелінійна регресія

Якщо графік регресії 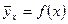або зображується кривою лінією, то кореляцію називають криволінійною (нелінійною). Наприклад, квадратичні функції використовуються для опису дуже широкого спектру економічних процесів, завдяки їхнім універсальним властивостям. Дійсно, у загальному випадку квадратична функція має вигляд:

. (1)

Обернена функція має вигляд:

, (2)

тобто узагальнені регресії моделі відповідно будуть:

, (3)

а вибіркові нелінійні регресії є

(4)

(5)

За методом найменших квадратів параметри знаходять з системи:

, (6)

(7)

Для аналізу зв’язку y і х в цих випадках використовуються кореляційними відношеннями:

, (8)

де .

Поиск по сайту: