Числові характеристики випадкових величин

Відомо, що закон розподілу повністю характеризує випадкову величину з ймовірносної точки зору. Знаючи закон розподілу випадкової величини, можна вказати, де розміщуються можливі значення випадкової величини і яка ймовірність появи її в тому чи іншому інтервалі.

Проте при розв’язанні багатьох задач нема необхідності характеризувати випадкову величину повністю, а досить мати про неї тільки деяке загальне уявлення. Часто буває досить вказати не весь закон розподілу, а лише його деякі характерні риси.

В теорії ймовірностей для загальної характеристики випадкових величин використовуються деякі величини, що носять назву числових характеристик випадкової величини.

Основне їх призначення – в стислій формі виразити найбільш суттєві особливості того чи іншого розподілу.

Про кожну випадкову величину необхідно перш за все знати її деяке середнє значення, біля якого групуються всеможливі значення випадкової величини, а також яке-небуть число, що характеризує ступінь розкидання (розсіювання) цих значень відносно середнього. Крім вказаних числових характеристик, для більш повного опису випадкової величини використовують і ряд інших характеристик. Всі вони допомагають в певній мірі вияснити характерні риси розподілу випадкової величини. Розглянемо найбільш часто вживані числові характеристики.

1. Математичне сподівання. Математичне сподівання є важливою характеристикою розміщення випадкової величини, його часто називають просто середнім значенням випадкової величини.

Розглянемо спочатку дискретну випадкову величину Х, що має всеможливі значення х₁, х₂, …х_n з ймовірностями р₁, р₂^,, …р_n.

Тоді математичне сподівання випадкової величини Х, яке позначають визначається рівністю:

. (1)

Якщо дискретна випадкова величина Х приймає нескінченну зліченну множину значень х₁, х₂, …х_n… з ймовірностями р₁, р₂^,, …р_n…, то її математичне сподівання є:

. (2)

Отже, математичним сподіванням випадкової величини Х називається сума добутків всіх можливих значень випадкової величини на ймовірності цих значень.

Надалі поряд з позначенням будемо використовувати позначення математичного сподівання через :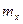

.

Нижче буде показано, що математичне сподівання наближено рівне середньому арифметичному спостережуваних значень випадкової величини, і тим точніше, чим більше число спостережень.

Розглянемо приклад, який з’ясовує доцільність прийнятого означення математичного сподівання.

Приклад1. Для розіграшу лотереї було випущено 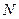білетів, з них з виграшем грн., білетів з виграшем грн., … білетів з виграшем грн. . Яка ціна білета, якщо сума грошей, виручених від продажу білетів, дорівнює сумі усіх виграшів?

Рішення. Якщо позначити шукану ціну білета через 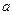, то за умовою:

,

звідки

,

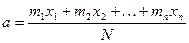тобто ціна одного білета дорівнює “середньому виграшу”. Останню формулу можна записати й інакше. Покладемо , очевидно, - це ймовірність того, що на вибраний наугад білет, випаде виграш 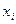грн. Тоді ця формула запишеться так:

.

Розглянемо тепер неперервну випадкову величину Х, значення якої належать відрізку 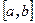. Нехай 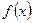є щільністю розподілу величини Х. Розбиваємо відрізок 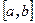на частинних відрізків довжиною . Візьмемо в кожному з таких відрізків по точці .

Так як добуток 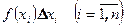наближено рівний ймовірності попадання випадкової величини на відрізок 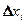, то сума добутків

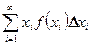, (3)

складена по аналогії з означенням математичного сподівання для дискретної випадкової величини, наближено рівна математичному сподіванню неперервної випадкової величини .

Якщо перейти до границі в сумі (3) при , отримаємо означений інтеграл, який і беруть за означенням рівним математичному сподіванню випадкової величини .

Якщо значення неперервної випадкової величини належать всій числовій осі, то математичне сподівання визначається інтегралом

. (5)

Приклад 2. Неперервна випадкова величина задана густиною (щільністю) розподілу:

Знайти значення параметра 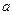та математичне сподівання випадкової величини .

Рішення. Параметр 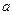знайдемо, користуючись властивістю 4 густини з §1.

.

Відмітимо найпростіші властивості математичного сподівання.

Властивість 1. Математичне сподівання постійної величини рівне самій постійній, тобто

.

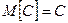Доведення. Сталу можна розглядати як дискретну випадкову величину, що набуває лише одне значення з ймовірністю 1.

Тому .

Властивість 2. Сталий множник можна виносити за знак математичного сподівання:

.

Доведення. Для дискретної випадкової величини маємо:

,

для неперервної:

.

Властивість 3. Математичне сподівання об’єднання двох випадкових величин дорівнює сумі їх математичних сподівань

.

Наслідок 1. Математичне сподівання об’єднання скінченного числа випадкових величин дорівнює сумі їх математичних сподівань:

.

Властивість 4. Математичне сподівання перетину двох незалежних випадкових величин дорівнює добутку їх математичних сподівань.

Поиск по сайту: