Дискретизація сигналу – теорема відліків (Котельникова)

Дискретизація функції в часі полягає в заміні даної неперервної функції іншою, решіткоподібною функцією, яка створена шляхом переривання початкової функції. Дискретизація можлива при умові, що новостворенна решіткоподібна функція дає можливість відновити початкову функцію. Ця умова виконується, якщо виконується теорема відліків, яка говорить, що будь-який неперервний сигнал, який має обмежений спектр, повністю визначається своїми дискретними значеннями в моменти відліків, які знаходяться один від одного в часі на інтервали 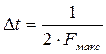, де F_макс – верхня частота обмеженого спектру неперервної функції.

Доведення теореми зводиться до наступного.

Будь – який фізично реальний, обмежений в часі сигнал може бути розглянутий як детермінований і неперіодичний сигнал і тим самим допускає вираження його зворотнім перетворенням Фур’є, тобто.

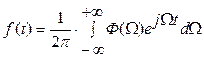, (4.27)

де Ф(W) – перетворення функції f(t) по Фур’є, тобто спектральна густина, або спектральна характеристика, функції f(t), є огибаючою амплітуд, які створюють спектр.

Так як неперервний сингал володіє обмеженим спектром (за формулювання теореми), то Ф(W) поза верхніми частотами, які обмежують спектр, рівна нулю, і вираз (4.27) приймає вигляд

. (5.1)

В моменти часу 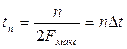, де n – цілі числа, а 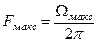, записана функція приймає значення

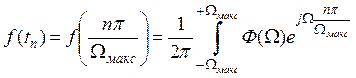.(5.2)

Спектральна густина функції Ф(W) – при умові, що ця функція періодично продовжена на всю вісь W - в свою чергу може бути подана рядом Фур’є, тобто

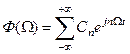. (5.3)

Так як розкладу належить неперервна функція частоти, то період вводиться в вираз для часу, тобто

(5.4)

значить,

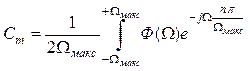. (5.5)

Порівнюючи вирази (5.2) і (5.5), видно, що

. (5.6)

Підставляючи отриманий результат в формулу (5.5) і враховуючи вираз (5.4), отримуємо

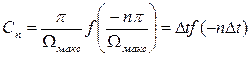. (5.7)

Тоді спектральна функція запишеться так:

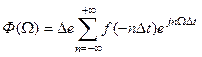. (5.8)

а вираз початкового коливання прийме вигляд

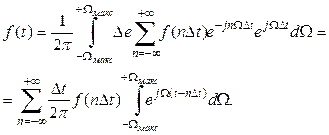(5.9)

В результаті інтегрування

.(5.10)

Враховуючи, що 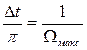, і використовуючи формулу Ейлера, дістаємо

. (5.11)

Останнє рівняння в аналітичній формі виражає функцію f(t) через її дискретні значення, взяті в моменти часу t_n, тобто з частотою F₀=2F_макс.

Теорема відліків являє собою в основному деяку математичну абстракцію, так як в ній говориться про сигнал з обмеженим спектром, в той час як будь-який обмежений в часі неперіодичний сигнал володіє безмежним спектром, тому на практиці частота дискретизації береться в 1.25 – 2.5 рази більше розрахованої. Такий вибір являє собою наслідок компромісу між наміром краще відтворити вихідний сигнал і умовою економії ширини полоси при передачі інформації.

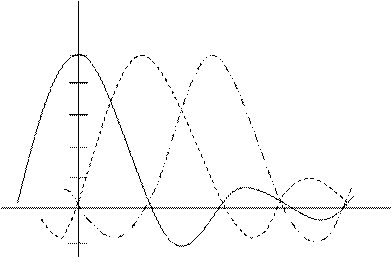Рисунок 5.1 – Графіки функції відліку

Для визначення будь-якого значення функції в проміжки між відліками необхідно проводити сумування всіх відліків, помножених на відповідні значення функцій відліків, які можуть приймати значення від –0.212 до +1. Більшою перевагою ряду є простота визначення його коєфіцієнтів (відліків). Цей ряд вперше був використаний в 1915 році Уіттакером.

Верхню частоту спектра неперервної функції часто вибирають, виходячи з умов збереження визначеної долі енергії, яка міститься в сигналах, які передаються.

Поиск по сайту: