Спектральний аналіз випадкових процесів

Введене для випадкових процесів поняття спектральної щільності автокореляційної функції, або енергетичний спектр функції B_ф(t), можна розглядати як спектральну щільність дисперсії, що є, у свою чергу, середньою потужністю, що виділяється на опорі в 1 ом. Ця потужність розприділяється по частотах в деякій смузі, що залежить від механізму утворення випадкового процесу і форми частотної характеристики ланцюга, через яку пропущений даний процес. Таким чином, розмірність енергетичного спектру є відношенням потужності до смуги частот.

Енергетичний спектр випадкового процесу можна знайти за параметрами імпульсів, які його утворюють. Визначення зводиться до сумування середніх квадратів окремих гармонічних складових (різних імпульсів), тобто енергетичний спектр визначається квадратом модуля спектральної густини елементарного імпульсу і середнім числом цих імпульсів за 1 сек.

Згідно формул (4.34) і (4.35),

. (4.56)

Ліва частина виразу – це формула енергії, що виділяється на опорі в 1 Ом. Допустимо, що f(t) є сумою двох функцій, що мають, кожна своє зображення по Фур’є. Тоді можна записати:

,

Розгортаючи обидві сторони виразу по формулах квадрату суми і використов`уючи рівність подвоєних похідних складових, одержуємо:

.

Припустивши далі, що f₂(t)=f₁(t+t) запишемо:

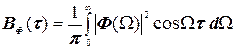, (4.57)

а прийнявши t=0, одержуємо:

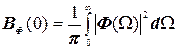. (4.58)

Формула (4.57) визначає автокореляційну функцію - В_ф(t) через квадрат модуля спектральної щільності функ­ції часу f(t), а формула (4.58) описує зв’язок функції В_ф(0) з энергією. Порівнюючи вирази (4.55) и (4.58), дістанемо:

. (4.59)

Чим менше тривалість імпульсів, що утворять випадковий процес, тим ширше енергетичний спектр процесу. Якщо тривалість імпульсів ринеться до нуля, то енергетичний спектр процесу стає рівномірним для всіх частот. Такий стаціонарний процес із рівномірним енергетичним спектром називається білим шумом.

Розглянуті залежності підтверджують, що автокореляційна функція містить повну інформацію про розподіл енергії процесу по частотах, але не дає зведень про частотний розподіл амплітуд і фаз спектральних складових реалізації процесу.

Шириною енергетичного спектра вважають інтервал частот, для котрого значення Ф₁(W) ще достатньо великі. Будь-які значення випадкового процесу варто вважати некорельованими лише в тому випадку, якщо процес має нескінченно широкий спектр. Обмеження спектра сигналу завжди збільшує кореляцію.

Частина п’ята

ДИСКРЕТИЗАЦІЯ ТА КВАНТУВАННЯ

Поиск по сайту: