Неперіодичні сигнали

Будь-який фізично реалізований сигнал із кінцевою енергією обов’язково обмежений у часу, або, іншими словами, функція, що зображує такий сигнал, абсолютно інтегрується. У зв’язку з цим неперіодичний сигнал може бути виражений відповідно модифікованою формулою періодичного сигналу. Модифікація, що зручно здійснити в комплексній формі запису, полягає в приравнюванні періоду коливаннь незкінченності і випливаючих із цього нескладних математичних перетворень.

Підставляючи вираз (4.19) у формулу (4.18), одержуємо:

Так як

(4.24)

то розподіл на нескінченно довгий період може бути замінено множенням на , що, у свою чергу, перетворює процес підсумовування в інтегрування і твір розмірів nW - у поточну частоту W. Отже,

. (4.25)

З цього виразу можна виділити величину

, (4.26)

який відіграє роль огибающей амплітуд, що складають спектр, і називається спектральною густиною, спектральною функцією або спектральною характеристикою відповідної неперіодичної функції. Вона іменується також прямим перетворенням даної функції по Фур’є. Вираз

, (4.27).

що подає залежність неперіодичної функцій від її спектральної характеристики, називається зворотним перетворенням Фур’є.

Порівнюючи комплексні форми запису періодичного і неперіодичного сигналів, одержуємо

. (4.28)

Це означає, що спектральну щільність Ф(W) можна одержати, якщо комплексну амплітуду n-й гармоніки розділити на смугу частот, що відокремлює сусідні лінії дискретного спектра, тобто Ф(W) дорівнює щільності амплітуд і має розмірність амплітуда на герц. Таким чином, що обгинає суцільного спектра (модуль спектральної щільності) неперіодичної функції й огибающая лінійчатого спектра періодичної функції збігаються за формою і відрізняються тільки масштабом. Спектральна щільність Ф(W) має всі основні властивості комплексної амплітуди С_n.

Коливання, що не задовольняють умовам Дірихле, не можуть бути подані перетворенням Фур’є, так як не існує відповідних їм спектральних функцій. Наприклад, f(t)=E при t³0 і f(t) = 0 при t<0. Для цієї функції

проте и при не наближається ні до якої межі, отже, спектральна функція не визначена. Причина в тому, що це коливання не є таким, що абсолютно інтегрується.

У таких випадках замість перетворення Фур’є вигідно користуватися так званим перетворенням Лапласа. Для цього перетворення коливання виражається так, щоб при t<0 f(t)=0. Суть перетворення складається у введенні поняття комплексної частоти, що дає можливість перебороти деякі математичні трудності. Комплексна частота позначається через р і виражається як

. (4.29)

Символічно перетворення Лапласа записуються у вигляді

, (4.30)

, (4.31)

а спектральна функція Ф(р) називається відображенням оригіналу f(t).

Виходячи з вище викладеного, пара перетворень Лапласа для неперіодичного сигналу може бути записана в такий спосіб:

(4.32)

і

, (4.33)

Перетворення Лапласа дає можливість розглядати й аналізувати прилади в умовах більш широкого класу коливань, чим це дозволяє перетворення Фур’є. Замінюючи у відображенні f(t) p на jW, можемо одержати відповідні спектральні функції.

Енергія, що виділяється неперіодичним сигналом на одноомному опорі, виражається формулою

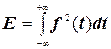. (4.34)

Записуючи її значення через модуль спектральної щільності сигналу Ф(W), можна визначити розподіл цієї енергії по спектрі неперіодичного коливання:

,

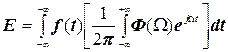що, міняючи порядок інтегрування, можна переписати у формі

,

або

.

Тому що добуток двох сполучених чисел дорівнює квадрату їхнього модуля, то

,

або

. (4.35)

Останній вираз відомо за назвою рівності Персеваля. Він визначає повну енергію, що виділяється сигналом f(t) за увесь час його існування. Середня потужність для будь-який абсолютно що інтегрується функції, рахуючи її період безкінечним, дорівнює нулю. Отже, |Ф(W)|² є енергія сигналу, що припадає на 1 гц поточної частоти W, або спектральна щільність енергії сигналу.

Формула (4.35) використовується для розрахунку необхідної смуги пропускання каналу зв’язку. Ця смуга позначається Q_макс і вибирається так, щоб її обмеженість не викликала втрат енергії, що перевищують припустимий розмір, наприклад 10%. Для цього щодо Q_макс вирішується рівняння

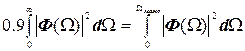. (4.36)

Коливання або сигнал f(t) завжди є дійсною функцією часу, проте компактність комплексних співвідношень призвела до частого використання комплексного представлення негармонійних коливань. Щоб таке подання було однозначним у усіх відношеннях, воно здійснюється аналітичними, або голоморфними, функціями. Вони, приходячи за формою функціями двох незалежних змінних х и у, фактично залежать тільки від комбінації цих змінних (x+jy), тобто є функцією однієї незалежної змінної z.

Аналітичність комплексної функції перевіряється умовами Коші-Рімана, відповідно до котрих щодо функції [Р(х,у) +j(x,y)] завжди повинні виконуватися рівності

Для досягнення аналітичності комплексної функції, за допомогою котрої бажано подати реальний сигнал , останній записується у формі

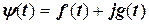(4.37)

як функція комплексного часу t+jt.

При цьому мниму частину виразу (4.37) варто обчислювати по формулі

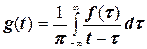(4.38)

і, отже,

. (4.39)

Співвідношення (4.38) і (4.39) називаються парою перетворень Гільберта. f(t) і g(t) іменуються сполученими коливаннями.

Для випадку гармонійного коливання дістаємо

,

а для випадку гармонійного коливання маємо

.

Таким чином, перетворення Гільберта для гармонійного коливання зводиться до його переміщення на 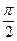у бік запізнювання. Якщо коливання f(t) складається із суми гармонійних коливань, то кожна гармонійна складова g_n(t) буде квадратурна (повернена нa 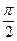у бік відставання) відповідної складової f_n(t). Хоча форми f(t) і g(t) різноманітні, проте коливання, що подаються ними, мають однаковий спектр амплітуд.

Поиск по сайту: