 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Кодування при відсутності перешкод
Кодом називається система відповідностей між дискретними елементами-символами повідомлень і сигналами, за допомогою яких ці елементи можуть бути зафіксовані або передані по каналу зв'язку. Таким чином, кодування полягає в представленні повідомлення, що передається послідовністю відносно простих електричних сигналів.
Кожному символу (букві алфавіту) може бути присвоєна своя величина електричного сигналу і тоді текст, що передається, буде складатись з m таких величин. Кількість букв алфавіту буде співпадати з кількістю можливих значень сигналів m -основою коду. Такий спосіб кодування при наявності перешкод енергетично невигідний, так як при його використанні максимальний імпульс повинен по напрузі перевищувати перешкоду в 2 m рази, або по енергії – в 4 m² рази. Тому вигідніше використовувати коди, основа m яких значно менша ніж кількість букв алфавіту. В цьому випадку кожна буква алфавіту передається цілою кодовою групою. В результаті кількість сигналів n, які передаються збільшується, але зменшується загальна кількість їх значень. Особливо вигідний в цьому відношенні двійковий код (m =2), заснований на двійковій системі числення, в якій будь-яке число А представляється в вигляді суми степенів числа 2:
А=а к 2к + а к-1 2к-1 +…+а12 + а0(3.1)
Коефіцієнти ак тут приймають значення виключно 0 або 1. Такі коефіцієнти називаються двійковими знаками. Перехід від десяткової системи числення на двійкову здійснюється таким чином:
відповідно виражене в десятковій системі число багатократно ділиться на 2 і отримані при кожному діленні остачі записуються справа наліво. Наприклад: 12110=11110012
Неперервні повідомлення спочатку дискретизуються по часу і квантуються по значеннях інформативного параметру, а потім передаються кодово-імпульсною модуляцією (особливо в телеметрії, управлінні, зв’язку).
При відсутності перешкод представляється доцільним створити такий код, який в середньому буде мати найбільш короткі кодові групи і одночасно повністю виключає будь-яку багатозначність. Таке кодування називається оптимальним. В результаті його здійснення можуть бути одержані рівномірні і нерівномірні коди. Рівномірним називається код, всі комбінації якого містять однакову кількість знаків; нерівномірним – такий, комбінації якого розрізняються по своїй довжині.
Прикладом оптимального коду є код Фено. Для кодування цим кодом всі елементи повідомлення діляться на дві групи, які позначаються 1 і 0, потім кожна з цих груп знову ділиться на дві підгрупи і так далі до тих пір, поки всі підгрупи не будуть містити по одному елементу повідомлення. Ділення на підгрупи повинно проводитись так, щоб сумарні ймовірності підгруп були по можливості однаковими. Наприклад, група з шести букв повинна кодуватися як показано в табл.3.1
Помилки через неоднозначності неможливі, так як ні одна довга кодова група не співпадає в своєму початку з короткою.
Таблиця 3.1 – Таблиця кодування кодом Фено
| Елементи, які кодуються | Ймовірність їх появи | Поступове утворення кодових комбінацій | ||||
| А | 0.25 | |||||
| Б | 0.15 | |||||
| В | 0.20 | |||||
| Г | 0.05 | |||||
| Д | 0.05 | |||||
| Е | 0.30 | |||||
| 1.00 |
Економічність створеного коду характеризується середньою кількістю розрядів (nср) на кодуючий елемент і розраховується за формулою:
 (3.2)
(3.2)
де рк – ймовірність появи елемента, який кодується; nk – кількість знаків в кодовій комбінації елемента; N – кількість елементів, які кодуються.
Розрахована величина ncp, у випадку двійкового коду, в своїй границі прямує до ентропії сукупності кодуючих елементів, що розраховуються за формулою:
 (3.3)
(3.3)
Середнє число розрядів на кодуючий елемент досягне значення ентропії, якщо в процесі кодування розбиття елементів на групи буде здійснено із точним дотриманням рівності ймовірностей цих груп. При будь-якому відступі від цього закону nср стає більше ніж Н, тобто
 (3.4)
(3.4)
У випадку, наведеному в табл. 3.1,отримуємо
nср=0,25·2+0,15·3+0,20·2+0,05·4+0,05·4+0,30·2=2,35 (біт/елем). Н=-0,25·log20,25+0,15·log20,15+0,20·log20,20+
+2·0,05·log20,05+0,30·log2 0,30)= 2,32 (біт/елем).
Невелика різниця обох значень викликана неточним співпаданням ймовірностей створених підгруп, а саме на другому етапі розбиття виникли підгрупи, що створені із елементів з ймовірністю 0,2(“В”) і з ймовірністю 0,3(“Е”), а на третьому етапі ймовірності підгруп виявились рівними 0,15 і 0,10.
У випадку рівноймовірності кодуючих елементів правило розбиття на підгрупи спрощується: підгрупи об’єднується по можливості в однакову кількість елементів. Спрощуються також формули (3.2) і (3.3), які приймають вигляд:
 (3.5)
(3.5)
 (3.5)
(3.5)
Чим більша сукупність кодуючих елементів, тим легше здійснити наближення середнього числа розрядів на кодуючий елемент до значення ентропії. Тому для підвищення економічності коду часто вдаються до штучного збільшення числа кодуючих елементів, об’єднюючи їх в блоки і визначаючи для кожного блоку свою кодову групу.
Наприклад, у випадку двох кодуючих елементів – А і Б з ймовірностями відповідно 0,8 і 0,2, надаючи цим елементам відповідно символи 1 і 0, одержуємо nср=1біт/елем при ентропії сукупності кодуючих елементів Н=0,722 1біт/елем. Здійснюючи об’єднання елементів попарно, одержуємо випадок, відображений в табл. 3.2.
Таблиця 3.2 – Об'єднання елементів попарно
| Пари, що кодуються | Ймовірність їх появи | Кодові комбінації, що створюються поступово | |||
| АА АБ БА ББ | 0,8. 0,8=0,64 0,8. 0,2=0,16 0,2. 0,8=0,16 0,2. 0,2=0,04 |
 | |
 |
В результаті:
2ncp= 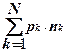 =0,64·1+0,16·2+0,16·3+0,04·3=1,56 (біт/2елем), або ncp =0,78 (біт/елем).
=0,64·1+0,16·2+0,16·3+0,04·3=1,56 (біт/2елем), або ncp =0,78 (біт/елем).
Відображені в таблиці 3.2 дії називаються кодуванням по методу n-грам. Досягаючий таким чином ефект формулюється основною теоремою кодування, де сказано, що при кодуванні повідомлення, розбитого на блоки по N1 елементів в кожному, можна, вибравши N1 достатньо великим, добитися того, щоб середнє число двійкових елементів сигналів (бітів) на один елемент вихідного повідомлення було як завгодно близьким до ентропії сукупності кодуючих елементів.
Крім коду Фено, оптимального в умовах відсутності перешкод, практично розповсюджений цілий ряд так званих первинних, або простих, кодів. Загальною рисою при їх створенні являлось прямування до мінімальної надлишковості з врахуванням технічних особливостей використання кодів. Найбільш давнім є континентальний код Морзе (1891р.). Це нерівномірний код, за допомогою якого окремі елементи повідомлення кодуються послідовністю крапок, пауз і тире. Тривалості цих елементів відносяться один до одного, як 1:1:3. Комбінації відділяються одна від одної інтервалом з тривалістю тире, а слова – інтервалами, рівними п’яти крапкам. При складанні континентального коду Морзе статистика української мови не враховувалась – найбільш короткі комбінації були виділені для літер, що часто зустрічаються у європейських мовах латинської письменності. Побудова коду Морзе для української мови дозволила б скоротити середню довжину кодових комбінацій від 8,65 до 7,68 елементів (на 11%).
Розробка конструкцій літеродрукуючих телеграфних апаратів потягнула за собою розвиток рівномірних кодів, тобто кодів, в яких усі літери передаються однаковою кількістю посилок.
Після введення багатократних телеграфних апаратів Бодо пануюче положення завоював п’ятизначний телеграфний код Бодо, який з незначними змінами був прийнятий в 1931році Міжнародним консультативним комітетом по телеграфії (МККТ)* у вигляді єдиного коду для телеграфії. В наступному, 1932 році був прийнятий стандартний код N2. Він містить всі основні символи, що необхідні для забезпечення телеграфного обміну, як вважав МККТ. З 1 січня 1968 року почав діяти новий стандарт СРСР на єдиний первинний код для передачі і обробки телеграфної інформації даних. Новий міжнародний код повинен поступово замінити існуючий стандартний первинний код – міжнародний телеграфний код N2. На відміну від коду N2 новий код семизначний. Основні труднощі його міжнародного впровадження були зв’язані з відмінністю абеток, а саме різною кількістю літер в абетках: 31 – в українській і 26 – в латинській.
Поиск по сайту: