Одиниці вимірювання інформації і інформативності

Будь-яке повідомлення, що передається, утримує в собі обмежену кількість інформації про будь-яку подію. “Подія” при цьому розуміється в самому широкому розумінні цього слова. Кількість інформації, що передається або одержується, прийнято зв'язувати із ступінню несподіваності події, про яку говориться в повідомленні. Чим несподіваніша подія, тим більше інформації в повідомленні про неї.

При такій постановці питання для надання поняттю “кількість інформації” чіткого математичного сенсу потрібно перш за все дати чіткий числовий вираз “степені несподіваності” повідомлення. Ця задача вирішується методами теорії імовірності.

Якщо по каналу зв'язку передати повідомлення про подію, ймовірність якого до передачі (апріорна) була р₁, а після прийому повідомлення стала (апостеріорна) рівною р₂, то приріст кількості інформації, що пов'язаний з прийомом повідомлення, визначається співвідношенням цих ймовірностей і одержана кількість інформації визначається формулою:

. (2.1)

Застосування логарифмічної функції для кількісної оцінки приросту інформації дає істотні переваги: так, повна інформація, яка міститься в повідомленні, що складається із декількох елементів, може бути одержана додаванням кількості інформації, що міститься в цих елементах. Крім того, якщо канал зв'язку ідеальний, тобто в ньому відсутні перешкоди та викривлення і, отже, прийняте повідомлення цілком достовірне, то приведений вираз справджується, так як імовірність

,

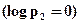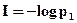. (2.2)

Так як початкова ймовірність завжди знаходиться в межах між нулем і одиницею, кількість інформації завжди додатна.

Чисельна величина кількості інформації залежить від вибору основи логарифма. Враховуючи, що технічні засоби передачі і злічування дискретної інформації частіше за все можуть приймати тільки два різних стани, вигідно користуватися логарифмом з основою 2. Тоді одиниця кількості інформації відповідає повідомленню про те, що трапилась одна з двох рівноймовірних подій. Вона називається двійковою одиницею інформації, або бітом.

Користуючись логарифмом з основою 10, одержуємо кількість інформації в інших одиницях — дітах, а користуючись натуральним логарифмом з основою е

, — в нітах.

Викладене ілюструє наступний приклад. Якщо по каналу зв'язку рівномірним кодом передається повідомлення про одну з восьми рівноймовірних подій, що здійснилися, кодові позначення ймовірності яких приведені в таблиці 2.1, то представляється можливим обчислити кількість інформації, що доставляється кожним наступним символом кодової групи, що передається. Для цього в першу чергу визначають ймовірності поступання окремих повідомлень після передачі кожного символу кодової групи (як це зроблено в таблиці 2.1), а потім розраховується кількість інформації, перенесеної кожним символом.

Таблиця 2.1 – ймовірності появи повідомлення

При передачі повідомлення 3 в першому символі міститься інформація[1]

,

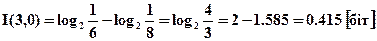в другому символі

,

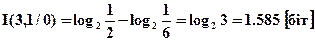в третьому символі

.

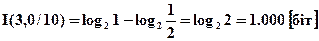Сумарна інформація дорівнює логарифму від величини оберненої апріорної імовірності повідомлення 3. Поряд з абсолютною кількістю інформації, що міститься в повідомленні, використовується поняття питома інформативність, або ентропія повідомлення. Під цим розуміється середня кількість інформації, що припадає на один символ передачі:

. (2.3)

Ентропія характеризує повідомлення з точки зору його насиченості інформацією. Чим більша ентропія повідомлення, тим більше інформації отримується за одиницю часу.

Поиск по сайту: