Пропускна здатність каналу

Під пропускною здатністю каналу приймається найбільше значення швидкості передачі інформації, яке може бути досягнуте в розглядуваному каналі.

Згідно цього визначення, позначивши пропускну здатність каналу через С, можна записати:

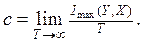(7.1)

В приведеній формулі І_мах(Y,X) - кількість інформації, одержаної приймачем Y від передавача X. Вона може бути виражена таким чином:

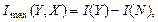(7.2)

де I(Y) - кількість інформації, що поступила в приймач;

I(N) - адитивна перешкода(завада), яка діє в каналй передачі.

Максимальне значення швидкості передачі визначається з максимальної кількості інформації, яка може поступити на приймач. Останнє випливає з ентропії самого інформативного реального сигналу. Таким являється неперервний сигнал, густина ймовірностей розподілу станів якого відповідає нормальному(гауссовому) закону. Його ентропія виражається формулою (2.32), а число незалежних елементів повідомлення за час Т, провівши дискретизацію сигналу згідно теореми Котельникова, можна записати як

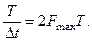(7.3)

Отже, 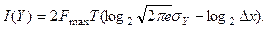(7.4)

З отриманого виразу далі слід відняти сприйняту приймальним пристроєм кількість інформації, що породжується шумами. З врахуванням найшкідливіших із-за своєї інформативності флуктуаційних шумів можна записати:

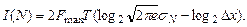(7.5)

Звичайно, кількість елементів повідомлення 2F_maxT і крок квантування Dx в обох випадках однакові, і формули відрізняються тільки значеннями середнього квадратичного відхилення s, яке у виразі (7.4) характеризує сигнал (s_Y), а у виразі (7.5) - шум (s_N).

В підсумку максимальна кількість інформації, що поступила на приймач від передавача, виражається формулою:

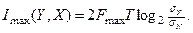(7.6)

Враховуючи, що дисперсія прийнятого повідомлення

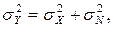(7.7)

а відношення дисперсії може бути замінене відношенням потужностей, отримаєм

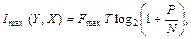(7.8)

де Р- середнє значення потужності повідомлення, яке передається;

N - середнє значення потужності перешкоди.

Підставляючи отриманий вираз (7.8) в формулу (7.1), запишемо:

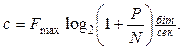(7.9)

Цей вираз відомий як формула Шеннона і визначає максимальну швидкість передачі інформації по каналу, що забезпечує пропускання частот до F_max при заданій середній потужності сигналу.

Характер зміни С в залежності від P/N визначається порядком відношення P/N. Так, якщо 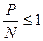, то допустима розгортка в такий ряд

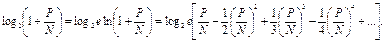(7.10) Враховуючи, що 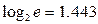і що при 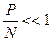записаний в дужках ряд вироджується в значення P/N, слідує, що для 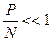маємо

с=1.443 F_max 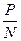. (7.11)

При малому значенні відношення сигнал-перешкода пропускна здатність каналу прямопропорційна цьому співвідношенню. Якщо 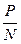>>1, то додавання до цього відношення одиниці стає неістотним і тому можна записати:

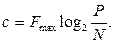(7.12)

При великих значеннях відношення сигнал-перешкода маємо логарифмічну залежність С від вказаного співвідношення.

Залежність пропускної здатності від полоси частот формулою (7.9) розкрита не повністю, так як в реальних системах має місце рівномірне розприділення перешкод (шумів) по всьому спектру. Отже, збільшення смуги частот тягне за собою збільшення рівня перешкод. Припустимо, що

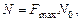(7.13)

де N₀ - спектральна густина потужності перешкод, і виражаючи потужність сигналу через N₀ в формі

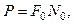(7.14)

отримаєм: 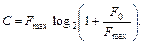(7.15)

З приведеної форми запису (7.15) видно, що збільшення F_max не дає необмеженого росту пропускної здатності каналу, яка прямує до межі, що досягається при 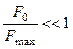. Граничне значення

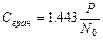. (7.16)

Таким чином, збільшення пропускної здатності каналу завжди досягається шляхом збільшення потужності передаючого пристрою і зменшення шумів. В той же час більший інтерес представляє проблема передачі повідомлень при малому значенні відношення сигнал-шум в широкій смузі частот.

Поиск по сайту: