Завадостійкість різних видів модуляції

При модуляції один з параметрів переносника міняється відповідно до характеру переданого сигналу. Отже, кожен переносник може бути модульований стількома видами модуляції, скільки параметрів він має. Зміна параметрів переносника в процесі передачі називається паразитною модуляцією. Визначення завадостійкості різних видів модуляції зводиться до визначення ступеня впливу малої адитивної перешкоди (паразитної модуляції) на інформативний сигнал, що переноситься різними прийомами (з використанням різних видів модуляції).

З цілю рішення цієї задачі припускаємо, що переносник у місці передачі в загальному виді описується своїми параметрами:

f(t)=f(a₁, a₂, …, a_n, t) (8.5)

На прийомному кінці той же переносник приймається разом з деякою малою адитивною перешкодою, що може бути записане в такий спосіб:

F(t)=f(a₁, a₂, …, a_n, t)+x(t) (8.6)

Тому що зазначена перешкода x(t) до деякої міри впливає на всі параметри переносника, то можемо її приставити розподілену між цими параметрами, тобто

F₁(t)=f(a₁+da₁, a₂+da₂,…, a_n+da_n, t) (8.7)

Якщо приведений тут розподіл зроблений правильно, то збільшення по кожному параметрі є його паразитною модуляцією і відношення сигнал/перешкода виражається формулою

q_k=(Da_k/da_k)² (8.8)

де Da_k — найбільший припустимий приріст параметра від корисної модуляції.

Порівнюючи вираз (8.8) для різних видів модуляції, одержуємо представлення про їхні завадостійкості. Чим більше одержуване повідомлення, тим завадостійкіший відповідний йому вид модуляції.

Рішення поставленої задачі зводиться до визначення δα_k для кожного виду модуляції, тобто правильному розподілу перешкоди по параметрах сигналу. Математично правильність розподілу може бути визначена як досягнення мінімуму величини d²: ________

d²=[F₁(t)-F(t)]² , (8.9)

що позначає мінімальну різницю між значенням сигналу, у якому перешкода розподілена по параметрах, і сигналу, до якого вона просто приплюсована. Мінімум приведеної у формулі (8.9) різниці досягається, якщо збільшення окремих параметрів (унаслідок паразитної модуляції) розраховані з виражень, у яких часткові похідні різниць (з формули (8.9)) по збільшеннях параметрів прирівняні до нуля.

Для цього величину d² виражаємо з урахуванням формул (8.6) і (8.7):

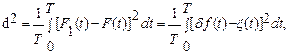(8.10)

де Т – інтервал усереднення, а

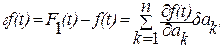(8.11)

що справедливо при малій перешкоді.

Таким чином, вираз (8.10) може бути переписаний у виді

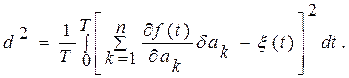(8.12)

Далі визначаються і прирівнюються нулю частинні похідні по збільшеннях окремих параметрів:

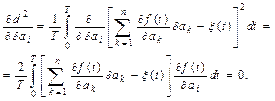(8.13)

Останнє справедливо, тому що з усієї суми тільки один член залежить від da_i. Це член, що містить da_i. З виразу (8.13) випливає:

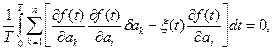(8.14)

а після введення нового позначення

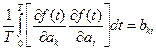, (8.15)

одержуємо

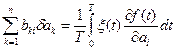. (8.16)

Останній вираз являє собою систему лінійних рівнянь, загальне рішення якої вигідно проілюструвати на двох рівняннях:

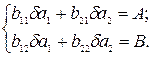(8.17)

Множачи перше з рівнянь (8.17) на b₂₂, а останнє на b₂₁, одержуємо:

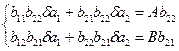(8.18)

і, віднімаючи друге від першого, записуємо

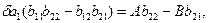
чи

, (8.19)

Виразивши отримане рішення в категоріях матриці величин b_ki, можемо стверджувати, що

(8.20)

де D-визначник матриці b_ki;

D_1i —алгебраїчне доповнення елемента b_1i, одержане в результаті множення його мінору на множник (-1)^k+1.

У загальному виді формулу (8.20) можна переписати як

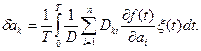(8.21)

Увівши ще одне нове позначення

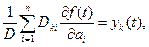(8.22)

можна записати:

(8.23)

Тоді

(8.24)

Але оскільки для перешкоди з рівномірним спектром

(8.25)

де N-потужність перешкоди, а

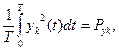(8.26)

де P_yk – потужність функції y_k(t), то вираз (8.24) може бути записаний у виді

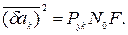(8.27)

Застосовуючи отримані висновки для співставлення завадостійкості амплітудної і частотної модуляцій гармонійної несучої, одержуємо f(t)=Asinwt, і відповідно a₁=A, a₂=w. У цьому випадку частинні похідні переносника, необхідні для запису матриці елементів b_кі, мають вид

.

Складові матриці b_кі,за умови що wT=np>>1, визначаються в такий спосіб:

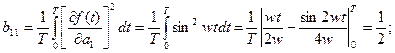
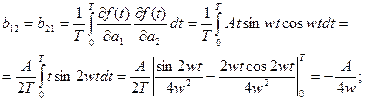
(другий член може бути опущений як мала величина іншого порядку). У такий спосіб матриця b_кі, одержує вид

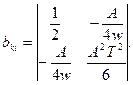
Її визначник D=A²T²/12. а відповідні алгебраїчні доповнення D₁₁=A²T²/6, D₁₂=D₂₁=A/4w, D₂₂=1/2. Функції у_к(t) мають значення:

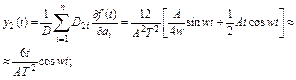
Потужності, що відповідають функціям у_к(t), одержують значення

;

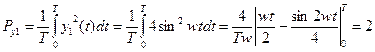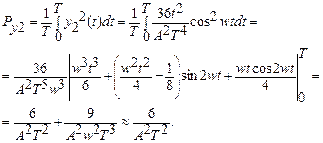
Усереднені значення потужності перешкоди у випадках амплітудної і частотної модуляцій відповідно рівні

__ __

da₁²=P_y1N₀F=2N₀F; da₂²=6N₀F/A²T².

отже, відношення сигнал/перешкода за умови, що глибина АМ складає 100%, одержує значення

q_AM=(Da₁)²/da₁²=A²/2N₀F=q,

що відповідає відношенню потужностей корисного сигналу і перешкоди для випадку модуляції синусоїдальним сигналом. Для ЧМ це ж співвідношення виражається як

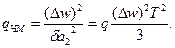
Оскільки девіація Dw_ЧМ= m_ЧМ W=2pnFm_ЧМ, де m_ЧМ – індекс частотної модуляції, а інтервал усереднення, по теоремі Котельникова, T=1/2F,то q_ЧМ=3,3m²_ЧМ.

Таким чином, відношення сигнал/перешкода у випадку частотної модуляції виходить у 3,3 m² разів більше, ніж у випадку амплітудної модуляції. Такий виграш у завадостійкості досягається за рахунок розширення спектра модульованого сигналу.

Поиск по сайту: