 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Циклічні коди. Циклічні коди були створені у пошуках більш простішої техніки кодування і декодування
Циклічні коди були створені у пошуках більш простішої техніки кодування і декодування. Для складання циклічного коду необхідні тіж вихідні дані, що і для складання систематичного коду. Відмінність полягає в тому, що систематичний код може бути складений для будь-якої комбінації (n, k), в той час як кількість можливих циклічних кодів фіксованої значності істотно обмежено, т.б. такі коди можуть бути здійснені тільки для цілком визначених комбінацій (n, k). Крім того, кількість кодових комбінацій, що реалізуються циклічним кодом, на одну менше кількості, що реалізується систематичним кодом, так як в циклічному коді не приймає участі нульовий вектор.
Основна властивість циклічних кодів, визначаюча їх назва, полягає в тому, що будь-який вектор v, що належить циклічному коду v, шляхом циклічної перестановки елементів останнього, теж може являтися дозволеною комбінацією того ж циклічного коду v. Під циклічною перестановкою при цьому розуміють послідовний перенос символів кодової комбінації з її кінця на перше місце.
В теорії кодування прийнято представляти вектори циклічних кодів y формі поліномів, а саме:
v(х) = а0 + а1х + а2х2 + … +аn-1xn-1. (3.20)
При такій формі представлення, що обмежується формальною умовою:
xn = 1, (3.21)
циклічну перестановку розуміють як множення приведеного полінома на х.
Складання циклічного коду починається визначенням продуктивного полінома g(x) степені n-k. Цей поліном звичайно береться з таблиць, в яких продуктивні поліноми циклічних кодів приведені для тих комбінацій (n,k), для яких вони існують. Даний поліном повинен виконувати одну єдину умову: на нього без залишка повинен ділитися двочлен 1+хn. (Дії над векторами виконуються по правилах арифметики по модулю 2, в якому віднімання рівносильно складанню.)
По продуктивному поліному будується продуктивна матриця. Вона містить k рядків. Перший рядок утворюють записані зліва направо коефіцієнти членів продуктивного полінома в порядку зростання показників їх степенів. Рядок доповнюється нулями з розрахунку, щоб вона містила n символів. Подальші рядки матриці одержуються шляхом циклічної перестановки символів. Решта N-k-1 кодові вектори одержуються як лінійні комбінації векторів, що входять в продуктивну матрицю.
Прикладом визначення кодових комбінацій може служити код з N=8, ρ=3 і показниками коду (7,4). Йому відповідає продуктивний, або генераторний, поліном
g(x) = g0 + g1х + g2х2 + … gn-kxn-k = 1 + x2 + x3. Продуктивна матриця тоді має вигляд:
 |
1 0 1 1 0 0 0
G = 0 1 0 1 1 0 0
0 0 1 0 1 1 0
0 0 0 1 0 1 1
Інші кодові вектори одержуємо як лінійні комбінації векторів, що входять в продуктивну матрицю. Позначаючи останнє відповідно через v 1, v 2, v 3 i v 4, можемо записати:
v1 + v 2 = 1 1 1 0 1 0 0
v 1 + v 3 = 1 0 0 1 1 1 0
v 1 + v 4 = 1 0 1 0 0 1 1
v 2 + v 3 = 0 1 1 1 0 1 0
Перевірка вимог, що пред’являються коду, як і у випадку систематичного коду, відбувається складанням матриці віддалей. Для приведеного прикладу вона має наступний вигляд:
1  2 3 4 5 6 7 8
2 3 4 5 6 7 8
2 0 4 4 4 3 3 3 3
3 0 4 4 3 3 7 3
4 0 4 3 3 3 3
5 0 7 3 3 3
6 0 4 4 4
7 0 4 4
8 0 4
9 0
Віддалі між кодовими комбінаціями у всіх випадках дорівнюють або більше 3. Отже, складений код задовільняє пред’явленим йому вимогам.
Для здійснення ефективного кодування і декодування необхідне знання перевірочного полінома h(x), який одержується діленням (по правилах арифметики по модулю 2) двочлена 1 + хn на генераторний поліном:

 (3.22)
(3.22)
Для приведеного прикладу одержуємо:
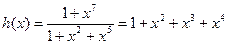
У випадку циклічних кодів можна при передачі користуватися скороченими кодовими комбінаціями, що складаються виключно з інформативних символів. Перевірочні символи додаються до цих комбінацій кодуючим пристроєм, що утворює вектори даного надлишкового коду. Інформаційними символами прийнято вважати останні k символи записаних кодових комбінацій, причому при вводі в кодуючий пристрій комбінації считуються справа наліво.
Кодуючий пристрій будується із зрушуючих регістрів у формі тригерних кіл з тими або іншими зворотніми зв’язками. Основними елементами схем є тригерні і сумуючі по модулю 2 комірки. На всіх схемах тригерна комірка позначається квадратиком, а сумуюча – кружечком із знаком „+” всередині. Дія тригерної комірки зводиться до того, що при дискретній дії на її вхід вона змінює свій стан.
Кожна така дія називається кроком. Під станом розуміється символ, що міститься всередині комірки. Після кожного кроку символи переміщуються по колу тригерних комірок.

Рисунок 3.3 – Кодуючий пристрій - k-ступеневий регістр
Кодуючий пристрій може здійснюватися у вигляді k-ступеневого регістра (рис.3.3). Згідно назві він містить k тригерних комірок із зворотніми зв’язками через сумуючі комірки. Наявність зв’язків визначається за допомогою перевірочного полінома. Реально існують тільки зв’язки, що відповідають коефіцієнтам перевірочного полінома, що дорівнюють одиниці: для нульових коефіцієнтів зв’язки відсутні.
Дія схеми зводиться до наступного. Ключ k першопочатково знаходиться в положенні 1, і протягом k послідовних кроків комірки регістра заповнюються послідовністю інформаційних символів (що зчитуються справа наліво). Потім ключ переводиться в положення 2 і протягом n-k кодових символів з одночасним утворенням в тригерних комірках n-k контрольних символів. Після цього ключ переводиться знову в положення 1, і протягом k кроків з регістра виводяться решта символи першої кодової комбінації і вводиться k символи наступної кодової комбінації і т.д.
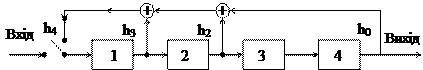 |
Рисунок 3.4 – k-ступеневий пристрій для полінома
H(x)=1+x2+x3+x4
Для приведеного прикладу схема k – ступеневого регістра (рис.3.4) при подачі на неї інформаційних символів, наприклад останнього, 8-го, кодового вектора, заповнюється в порядку, що показаний в табл.3.8.
Таблиця 3.8-Заповнення таблиці при подачі в регістр
інформаційних символів
| Після кроку | Комірки регістра | Вивід | ||||
| К = 4 К + 1 =5 К + 2 = 6 К + 3 = 7 | - | - | ||||
Кодування може відбуватися також n-k – ступеневим регістром (рис.3.5). В ньому n-k комірок; наявність зворотніх зв’язків визначається генераторним поліномом.
 |
Рисунок 3.5 – Кодуючий пристрій - (n-k)- ступеневий
регістр
Дія схеми зводиться до наступного. Обидва ключа першопочатково знаходяться в положенні 1, і на протязі k послідовних кроків всі інформаційні символи одночасно подаються безпосередньо на вихід і в кодуючий пристрій для утворення перевірочних символів. Потім обидва ключа переводяться в положення 2, і на протязі n-k кроків здійснюється вивід із схеми n-k контрольних символів. Потім ключі переводяться знову в положення 1 і т.д.
Для приведеного прикладу схема (n-k) – ступеневого регістра (рис.3.6) при подачі на неї інформаційних символів того ж останнього, 1-го, кодового вектора заповнюється в порядку, що показаний в табл.3.9.
 |
Рисунок 3.6 - (n-k) - ступеневий регістр для поліному
g(x)=1+x2+x3
Таблиця 3.9-Заповнення таблиці при подачі в регістр
інформаційних символів
| Після кроку | Комірки регістра | ||
| - |
В практичних реалізаціях перевага надається більш простому варіанту, т.б. у випадку розглянутого прикладу (n-k) – ступеневому кодуючому пристрї.
Декодуючий пристрій призначений виявляти і усувати помилки. Для виправлення однократних помилок він реалізується по схемі, аналогічній кодуючому пристрою. Єдина відмінність в тому, що зв’язки від g1 до gn-k-1 здійснюються не з вхідного, а з вихідного кола (рис.3.7). Вектор, що приймається, вводиться в декодуючу схему послідовними кроками. При відсутності помилки після закінчення прийому кодової групи регістр декодуючого пристрою заповнений нулями. Якщо хоча б одна комірка містить одиницю, це вказує на наявність помилки в прийнятій кодовій комбінації.
 |
Рисунок 3.7 – Декодуючий пристрій для виправлення
однократних помилок

Для встановлення місця однократної помилки декодуючий пристрій потрібно відключити від приймаючого апарата. Так щоб він продовжував працювати на „себе”. Номер кроку, на якому в першій тригерній комірці з’явиться одиниця, а в усіх решта – нулі, буде відповідати номеру викривленого символу (що зчитується справа наліво).
Рисунок 3.8 – Декодуючий пристрій для полінома
g(x)=1+x2+x3
Заповнення схеми декодуючого регістра (рис.3.8.) при подачі на неї останньої, 8-ої, кодовох комбінації показано в табл. 3.10.
У випадку викривлення п’ятого символу тієї ж комбінації одержуємо наступну картину, показану в табл. 3.11.
Конкретні відозміни циклічних кодів широко застосовуються також для виявлення пакетних помилок.
Таблиця 3.10 – Заповнення таблиці при подачі в регістр
інформаційних символів
| Після кроку | Комірки регістра | ||
| - | - - |
Таблиця 3.11 – Заповнення таблиці при подачі в регістр
інформаційних символів
| Після кроку | Комірки регістра | ||
При роботі „ на себе”



 1 1 0 1
1 1 0 1
2 1 1 1
3 0 1 0
4 1 1 1

 5 1 0 0
5 1 0 0
Поиск по сайту: