Циклічні коди

Циклічним кодом називається лінійний блоковий (n, k) код, який характеризується властивістю циклічності, тобто зсув ліворуч на один крок будь-якого дозволеного кодового слова дає також дозволене кодове слово, яке належить цьому ж коду і у якого безліч кодових слів подається сукупністю багаточленів степеня
(n –1) і менше, що діляться на деякий багаточлен G(x) степеня
r = n–m, що є співмножником двочлена xⁿ + 1.

Багаточлен G(x) називається породжувальним.

Як випливає з визначення, у циклічному коді кодові слова подаються у вигляді багаточленів

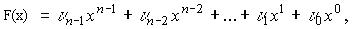
де n–довжина коду;

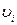–коефіцієнти з поля GF(q).

Якщо код побудований над полем GF(2), то коефіцієнти беруть значення 0 або 1 і код називається двійковим.

Циклічні коди прості в реалізації і при невисокій надмірності мають хороші властивості виявлення спотворень. Циклічні коди поширені як у техніці зв’язку, так і в комп’ютерних засобах зберігання інформації. У зарубіжних джерелах циклічні коди зазвичай називають перевіркою циклічним надмірним кодом (CRC, Cyclic Redundancy Check).

Розглянемо даний клас кодів докладніше. Як уже згадувалося, назва циклічних кодів пов’язана з тим, що кожна кодова комбінація, одержана шляхом циклічної перестановки символів, також належить коду. Так, наприклад, циклічні перестановки комбінації 1000101 будуть також кодовими комбінаціями 0001011, 0010110, 0101100 і т.д.

Подання кодових комбінацій у вигляді багаточленів F(x) дозволяє встановити однозначну відповідність між ними і звести дії над комбінаціями до дії над багаточленами.

Приклад. Якщо кодове слово циклічного коду

,

то багаточлен, відповідає йому:

.

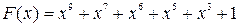Складання двійкових багаточленів зводиться до складання по модулю 2 коефіцієнтів при однакових степенях змінної x. Множення здійснюється за звичним правилом множення степеневих функцій, проте одержані коефіцієнти при даному степені складаються по модулю 2. Розподіл здійснюється як звичний розподіл багаточленів, при цьому операція віднімання замінюється операцією складання по модулю 2. Циклічна перестановка кодової комбінації еквівалентна множенню полінома F(x) на x із заміною на одиницю змінної зі степенем, що перевищує степінь полінома.

Особливу роль у теорії циклічних кодів виконують багаточлени G(x), що не приводяться, тобто поліноми, які не можуть бути подані у вигляді добутку багаточленів нижчих степенів. Вибір багаточленів G(x) здійснюється зі спеціальних таблиць з умови, щоби їх степінь була не меншою, ніж кратність можливих спотворень.

Ідея побудови циклічного коду (n, m) зводиться до того, що поліном Q (x), який подає інформаційну частину кодової комбінації, потрібно перетворити в поліном F (x) степені не більше (n –1), який без залишку ділиться на породжувальний поліном G (x) (багаточлен, що не приводиться) степені k = n - m. Розглянемо послідовність операцій побудови циклічного коду.<lt>

Подаємо інформаційну частину кодової комбінації завдовжки m у вигляді полінома Q (x). Для одержання k позицій під контрольні символи множимо Q (x) на одночлен x^k і одержуємо Q (x)∙ x^k.

Ділимо поліном Q (x)∙ x^k на породжувальний поліном G (x) степені k, при цьому одержуємо результат розподілу С (x) такої ж степені, що і Q (x). </lt>

,

де R (x) – залишок від розподілу Q (x)∙ x^k на G (x).

Помноживши обидві частини на G (x), одержимо

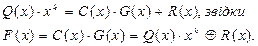
Поліном F (x) ділиться без залишку на G (x), тобто є дозволеною комбінацією циклічного (n, m) коду.

Приклад циклічного коду (9, 5) з породжувальним поліномом

.

Як інформаційну частину кодової комбінації візьмемо поліном

Q (x)= x⁴+ x²+ x +1 = 10111.

Множення Q (x) на x^k еквівалентне підвищенню степені багаточлена на k.

F(x)= Q (x )∙x^k = = .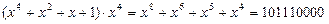

Формування перевірочної групи здійснюється в процесі розподілу Q (x)∙ x^k на G (x).

x8	+	x6	+	x5	+	x4	x4	+	x	+
x8	+			x5	+	x4		x4	+	x2
		x6
		x6	+	x3	+	x2
				x3	+	x2

У наслідок розподілу одержуємо результат С(x)= x⁴ + x² =
= 10100 і залишок від розподілу R (x)= x ³ + x ² = 1100. Для отримання дозволеної кодової комбінації залишок (перевірочна група) поміщається на місце «порожніх» розрядів Q (x)∙ x^k, тобто

F (x)= =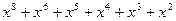
= 101111100.

Ця комбінація відправляється в канал зв’язку. Аналогічні операції виконуються для інших інформаційних комбінацій.

Виявлення помилок при циклічному кодуванні зводиться до розподілу прийнятої кодової комбінації на той же породжувальний поліном, який використовувався для кодування. Якщо помилок у прийнятій комбінації немає (або вони такі, що передану комбінацію перетворюють на іншу дозволену), то розподіл на породжувальний поліном здійснюється без залишку. Наявність залишку свідчить про присутність помилок.

При використанні в циклічних кодах декодування з виправленням помилок залишок від розподілу може виконувати роль синдрому. Нульовий синдром указує на те, що прийнята комбінація є дозволеною. Усякому ненульовому синдрому відповідає певна конфігурація помилок, яка і виправляється.

Зазвичай в системах зв’язку виправлення помилок при використанні циклічних кодів не здійснюється, а при виявленні помилок видається запит на повтор спотвореної помилками комбінації.

Для виправлення пакетів спотворень (три і більше помилки) розроблені коди Файра, Ріда-Соломона та ін. Останні можуть виправляти кілька пакетів помилок.

Поиск по сайту: