 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Згортальні двійкові коди
|
Читайте также: |
Згортальні (рекурентні, ланцюгові) коди належать до класу неперервних, оскільки як операції кодування, так і операції декодування здійснюються неперервно над послідовністю символів, яка не поділяється на блоки. Кожні n символів складаються, як і в інших кодах, з m інформаційних і k перевірочних. Перевагою кодів є можливість виявляти і виправляти групові спотворення.
Ці коди можуть мати різну надлишковість, але найпростіше вони реалізуються при m = k, тобто коли n = m + k = 2 m = 2 k, а відносна швидкість передачі дорівнює
R = m / k = m /2 m = 0,5.
У цьому випадку перевірки створюють послідовно пов’язані ланцюги, що й відображено в одній із назв коду «ланцюговий».
Згортальні (рекурентні, ланцюгові) коди використовуються для кодування неперервної послідовності двійкових символів шляхом уведення в цю послідовність спеціальних перевірочних символів. Наприклад, для кожного інформаційного символу вихідної послідовності (а), які є рознесеними між собою на крок додавання (кодування, перемежування) λ,формується один спеціальний перевірочний символ(п).
| Передавання | Приймання |

| 
|
| 
|
| … | … |

| 
|

| 
|
| і т. д. |
Передаються перевірочні символи з певною затримкою відносно інформаційних. На боці приймача із інформаційних символів ( ) формуються нові перевірочні, які на відміну від перевірочних символів
) формуються нові перевірочні, які на відміну від перевірочних символів 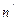 , які прийнято, називаються контрольними. Контрольні символи (к) порівнюються з перевірочними і в разі їх незбігання формується висновок про наявність спотворення. Перевірочні і контрольні символи формуються складанням по модулю 2 інформаційних. Одна перевірка охоплює ті інформаційні символи, різниця номерів яких дорівнює кроку додавання (глибині перемежування):
, які прийнято, називаються контрольними. Контрольні символи (к) порівнюються з перевірочними і в разі їх незбігання формується висновок про наявність спотворення. Перевірочні і контрольні символи формуються складанням по модулю 2 інформаційних. Одна перевірка охоплює ті інформаційні символи, різниця номерів яких дорівнює кроку додавання (глибині перемежування):
і + λ– і = і + λ + 1– (і +1) = і + 2λ + 1– (і +λ + 1) = …= λ.
Кожен контрольний символ порівнюється з відповідним перевірочним:
  ; ;
|
 
|
| і т. д. |
Ознакою відсутності спотворень є те, що усі суми дорівнюють нулю:

 …= 0.
…= 0.
Спотвореним може бути як інформаційний, так і перевірочний символ.
На спотворення одного перевірочного символу указує те, що одна із сум дорівнює одиниці. Наприклад, при спотворенні  отримаємо
отримаємо  , оскільки
, оскільки  не збігається з
не збігається з  . Якщо подальшої передачі цієї послідовності не здійснюється (ретрансляції немає), то ніяких виправлень здійснювати не слід.
. Якщо подальшої передачі цієї послідовності не здійснюється (ретрансляції немає), то ніяких виправлень здійснювати не слід.
Наявність двох сум, які дорівнюють одиниці і віддалені (зсунуті) між собою на крок додавання λ, свідчить про спотворення двох перевірочних символів.
Розглянемо приклад послідовного згортального коду з кроком додавання λ = 3 за умови, що перевірочні символи прийнято без спотворень. Нехай із спотворенням прийнято три інформаційних символи. Формування перевірочних і контрольних символів показано на рис. 5.1.

Рис. 5.1. Формування перевірочних і контрольних символів за наявності спотворення в символах з номерами 4, 5, 6
( Увага! Розташування перевірочних символів на цьому рисунку показано умовно і не відповідає вимогам до нього!)
Для заданих умов усі перевірочні символи дорівнюють нулю. У наслідок спотворення символів з номерами 4, 5, 6 серед контрольних символів, які формуються за участю спотворених, з’являються символи, що відрізняються від перевірочних, тобто дорівнюють одиниці.
Порівняємо контрольні елементи з перевірочними, які є прийнятими.
Видно, що утворилися три пари сум, які дорівнюють одиниці і зсунуті на крок додавання λ = 3:
 і
і  ;
;  і
і  ;
;  і
і  .
.
Звідси робимо висновок, що спотворені ті інформаційні символи, номери позицій яких є спільними в кожній парі сум, тобто а 4, а 5, а 5. Значення цих символів слід виправити на протилежні: прийнято 0–повинна бути 1 і навпаки. Отже, виправлено три спотворення, тобто кількість спотворень, що виправляються, дорівнює кроку додавання.

|

|

|

|

|
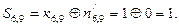
|
Із цього прикладу можна зробити і побічний висновок: значення λ визначає не лише крок додавання, а й глибину перемежування, тобто кількість окремих незалежних ланцюгів коду. Дійсно, при λ = 3 маємо три незалежних ланцюги:

|

|

|

Рис. 5.2. Формування перевірочних і контрольних символів за наявності спотворення в символах з номерами 1, 4, 5, 6, 12
Розглянемо ще один приклад. Значення інформаційних і перевірочних символів при передаванні–такі ж, як і в попередньому прикладі (див. рис. 5.1). Перевірочні символи прийнято без спотворень, з спотвореннями прийнято інформаційні символи 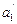 ,
,  ,
,  ,
,  ,
,  (рис. 5.2).
(рис. 5.2).
Результат порівняння контрольних і перевірочних символів покажемо для кожного з ланцюгів:
| перший ланцюг: |   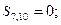 
|
| другий ланцюг: |   
|
| третій ланцюг: |   
|
З отриманих результатів додавання контрольних і перевірочних символів розглянемо можливість виправлення спотворень у кожному незалежному ланцюзі коду.
Перший ланцюг містить 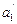 ,
,  ,
,  ,
,  ,
,  та відповідні перевірочні символи
та відповідні перевірочні символи  ,
,  ,
,  ,
,  . За умовою спотвореними є
. За умовою спотвореними є 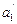 ,
,  . У цьому ланцюзі тільки одна із сум дорівнює одиниці:
. У цьому ланцюзі тільки одна із сум дорівнює одиниці:
 .
.
Виходячи з правил виявлення спотворень, можна стверджувати, що спотвореним є перевірочний символ  . Однак це суперечить умові прикладу: перевірочні символи прийнято без спотворень. Тобто виявлення спотворених інформаційних символів, які входять до першого ланцюга, не здійснено. Більш того, неправильно буде «виправленим» перевірочний символ
. Однак це суперечить умові прикладу: перевірочні символи прийнято без спотворень. Тобто виявлення спотворених інформаційних символів, які входять до першого ланцюга, не здійснено. Більш того, неправильно буде «виправленим» перевірочний символ  .
.
Другий ланцюг містить  ,
,  ,
,  ,
,  та
та  ,
,  ,
,  . За умовою спотворено
. За умовою спотворено  . Те, що в цьому ланцюзі дорівнюють одиниці дві суми (
. Те, що в цьому ланцюзі дорівнюють одиниці дві суми (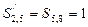 ), свідчить про спотворення одного інформаційного символу з спільним для цих сум індексом, тобто
), свідчить про спотворення одного інформаційного символу з спільним для цих сум індексом, тобто  . У другому ланцюзі спотворення буде виправлено правильно.
. У другому ланцюзі спотворення буде виправлено правильно.
У третій ланцюг входять 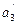 ,
,  ,
,  ,
,  та
та  ,
,  ,
,  . Згідно з умовою прикладу спотвореними є
. Згідно з умовою прикладу спотвореними є  та
та  . В цьому ланцюзі три суми дорівнюють одиниці
. В цьому ланцюзі три суми дорівнюють одиниці
 .
.
За рівнянням  можна виправити
можна виправити  ; рівняння
; рівняння  указує на спотворення
указує на спотворення  , що суперечить умові. Отже, спотворення
, що суперечить умові. Отже, спотворення  не виявлено і неправильно виправлено
не виявлено і неправильно виправлено  . Якщо узяти
. Якщо узяти  , можна вважати спотвореним
, можна вважати спотвореним  , що є також неправильним.
, що є також неправильним.
Розглянувши два приклади з різною кількістю спотворених інформаційних символів, можна зробити наступні висновки про те, що:
1. Якщо спотворення перевищує можливості коду, код не лише не здатен виявляти та виправляти спотворення, але й вносить додаткові спотворення:
2. Інформаційні символі одного ланцюга розташовуються на відстані λ інформаційних та λ перевірочних, отже, на відстані 2 λ символів один від іншого.
3. Місце розташування перевірочних символів визначається двома обставинами: по-перше, групова завада не повинна одночасно охоплювати інформаційні і відповідні перевірочні символи; по-друге, не повинно бути неправильного виправлення інформаційних символів.
Із цих міркувань перевірочні символи розташовуються на відстані 2 λ + 1 символів від найближчого свого інформаційного. Наприклад, перевірочний символ 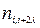 , створений з інформаційних
, створений з інформаційних  та
та  повинен займати [(i + 2λ) + 2 λ + 1 ] =
повинен займати [(i + 2λ) + 2 λ + 1 ] =
= (і + 4 λ + 1) позицію.
За таких умов згортальний код виправляє групове спотворення із λ інформаційних символів (див. перший приклад).
З викладеного раніше зрозуміло, що:
1. Інформаційні та перевірочні символи повинні чергуватися. Для визначеності будемо вважати, що інформаційні символи мають непарні номери, а перевірочні – парні.
2. Повинні бути сформованими два (λ = 2) незалежних ланцюги формування перевірочних (а в подальшому і контрольних) символів.
Оскільки рознесення між інформаційними символами кожного незалежного ланцюга складає λ інформаційних символів, то і відстань між відповідними перевірочними символами також дорівнює кроку додавання.
Важливою характеристикою згортального коду є мінімально допустима відстань між суміжними груповими спотвореннями, коли ще можна виправляти спотворень (див. рис. 5.3). Ця відстань повинна забезпечувати правильне приймання 2 λ інформаційних символів після спотворення та 2 λ перевірочних, які охоплюють спотворені інформаційні символи. Тому мінімальна допустима відстань дорівнює 4 λ + 1 символів.
 Рис. 5.3. Мінімально допустима відстань між груповими спотвореннями
Рис. 5.3. Мінімально допустима відстань між груповими спотвореннями
Оскільки в інформаційних повідомленнях, що передаються неперервно, перевірочні та інформаційні символи чергуються:  , п,
, п, 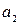 , п,
, п,  , …, то інформаційні символи, що входять у одну перевірку, рознесені поміж собою на λ інформаційних і λ перевірочних символів. Тобто при кроці додавання λ інформаційних символів згортальний код виправляє групове спотворення з b = 2 λ інформаційних і перевірочних символів, а мінімально допустима відстань між груповими спотвореннями дорівнює
, …, то інформаційні символи, що входять у одну перевірку, рознесені поміж собою на λ інформаційних і λ перевірочних символів. Тобто при кроці додавання λ інформаційних символів згортальний код виправляє групове спотворення з b = 2 λ інформаційних і перевірочних символів, а мінімально допустима відстань між груповими спотвореннями дорівнює
М = 4 λ +1 = 2 b + 1
інформаційних і перевірочних символів.
Поиск по сайту: