 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
МІНІСТЕРСТВО ОСВІТИ І НАУКИ. Класичне означення ймовірності появи події:
Класичне означення ймовірності появи події: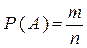 
.
Розміщення: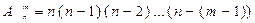 
.
Перестановки: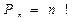 
.
Сполучення: 
.
Теорема додавання ймовірностей несумісних подій: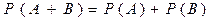 
.
Ймовірність повної групи подій: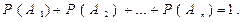 
Сума ймовірностей протилежних подій: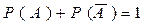 
.
Ймовірність сумісної появи двох подій: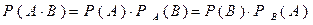 
.
Ймовірність сумісної появи двох незалежних подій: 
.
Ймовірність появи однієї з двох сумісних подій: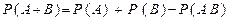 
.
Ймовірність появи хоча б однієї з подій: 
.
Формула повної ймовірності: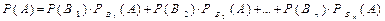 
.
Формули Бейєса: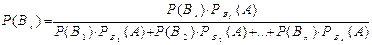 
.
Формула Бернуллі: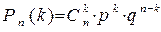 
.
Локальна теорема Лапласа: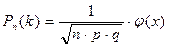 
, де 
.
Інтегральна теорема Лапласа: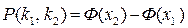 
, де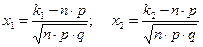 
.
Формула Пуассона: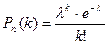 
, де 
.
Математичне сподіваннядискретної випадкової величини:
.
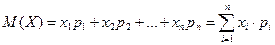Дисперсія дискретної випадкової величини: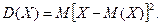 
.
Середнє квадратичне відхилення: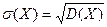 
.
Функція розподілу (інтегральна функція розподілу):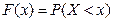 
.
Ймовірність того, що випадкова величина 
прийме значення із проміжку 
: 
.
Диференціальна функція розподілу: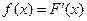 
.
Ймовірність того, що неперервна випадкова величина прийме значення з інтервалу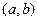 
: 
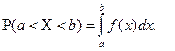
Зв’язок між інтегральною і диференціальною функціями розподілу: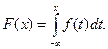 
Математичне сподівання неперервної випадкової величини: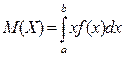 
.
Дисперсія неперервної випадкової величини: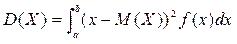 
,
.
Математичне сподівання при біноміальному законі розподілу: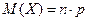 
.
Дисперсія при біноміальному законі розподілу: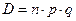 
.
Рівномірний розподіл ймовірності: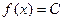 
.
Нормальний закон розподілу: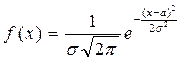 
.
Ймовірність попадання неперервної випадкової величини, розподіленої нормально, у заданий інтервал: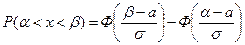 
.
Емпірична функція розподілу: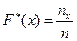 
.
Середня арифметична: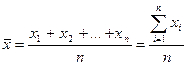 
,
.
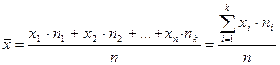Дисперсія: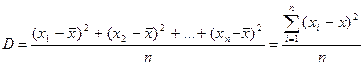 
,
.
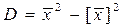
Коефіцієнт варіації: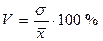 
.
Медіана при неперервному розподілі: 
.
Мода при неперервному розподілі: 
Коефіцієнт асиметрії: 
.
Ексцес або коефіцієнт крутості: 
.
Метод добутків: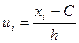 
, 
.
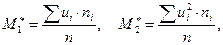
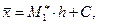
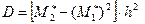Поправка Бесселя: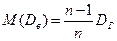 
.
Виправлена дисперсія: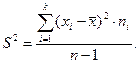 
Виправлене середнє квадратичне відхилення: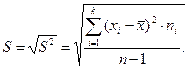 
Довірчий інтервал для оцінки математичного сподівання: 
.
Довірчий інтервал для оцінки середнього квадратичного відхилення: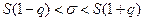 
.
Перевірка гіпотези про рівність дисперсій двох генеральних сукупностей:
, 
.
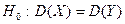1. 
, 
, 
, 
, 
.
Якщо 
, тоді немає підстав відкидати нульову гіпотезу. Якщо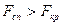 
, тоді нульову гіпотезу відкидаємо.
2. 
, , 
, , .
Якщо , тоді немає підстав відкидати нульову гіпотезу. Якщо 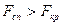, тоді нульову гіпотезу відкидаємо.
Перевірка гіпотези про нормальний розподіл генеральної сукупності. (Критерій згоди 
-Пірсона): 
, 
, 
, 
Якщо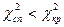 
, тоді немає підстав відкидати нульову гіпотезу. Якщо 
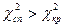, тоді нульову гіпотезу відкидають.
Методика обчислення теоретичних частот у припущенні нормального розподілу: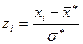 
, 
, 
, 
.
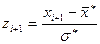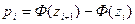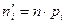Метод найменших квадратів: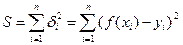 
.
Рівняння прямої: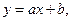 
.
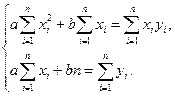Рівняння параболи: 
, 
.
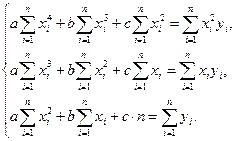Рівняння гіперболи: 
, 
, 
.
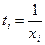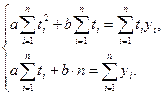Рівняння показникової функції: 
, 
, 
.
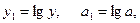
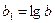Рівняння прямої лінії по згрупованим даним: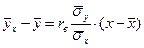 
.
Вибірковий коефіцієнт кореляції: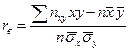 
.
МІНІСТЕРСТВО ОСВІТИ І НАУКИ
Поиск по сайту: