Прийом точно відомих сигналів

Сигнали є відомими точно, якщо невідомо лише і підлягає визначенню, який з ряду точно відомих сигналів мався на вході приймача протягом визначеного інтервалу часу. Оскільки визначення сигналу означає одночасне визначення відповідного йому повідомлення, надалі для стислості будемо вживати лише поняття сигнал.

Формула зворотної ймовірності, що обчислюється оптимальним приймачем, виходячи з загальних співвідношень теорії ймовірностей записується як

Р_у(х) = Р(х)Р_х(у)/Р(у), (8.40)

де Р(у) і Р(х) – відповідно безумовні ймовірності прийнятого сигналу у і переданого сигналу х, а Р_х(у) – умовна ймовірність у при даному х.

Оскільки при обчисленні Р_у(х) нас цікавить залежність цієї функції від х при незмінному у, то множник 1/Р(у) може бути замінений деякою константою k. Р(х) передбачається відомим як апріорна ймовірність сигналу х.

Р_х(у) називається функцією правдоподібності. При даному х імовірність реалізації сигналу у(t) збігається з ймовірністю такої реалізації перешкоди, що дорівнює різниці [y(t)-x(t)]. Ймовірність реалізації перешкоди характеризується щільністю цієї ймовірності. Якщо повідомлення про перешкоду статистично незалеже, одержуємо

Р_х(у)=φ_ш [y(t)-x(t)]. (8.41)

Щільність ймовірності перешкоди, що має характер білого шуму, для кожної частоти виражається одномірним законом розподілу шуму:

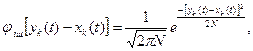(8.42)

що відповідає багатомірному закону

(8.43)

Відповідно до теореми Котельникова,

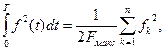(8.44)

а

N= FмаксN₀, (7.13)

вираз (8.41) представляється можливим переписати у формі

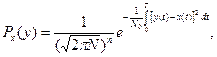(8.45)

а

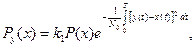(8.46)

що після елементарних перетворень з урахуванням сталості величин, що не залежать від х, може бути переписане у формі

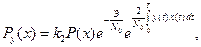(8.47)

чи

(8.48)

де Э – енергія сигналу, що несе повідомлення х; В₁₂ – величина, пропорційна функції взаємної кореляції сприйнятого і переданого сигналу;

(8.49)

Оскільки приймач діє за принципом максимальної зворотної ймовірності, то він відтворює щораз той сигнал, для якого зворотна ймовірність Р_у(х) виявляється найбільшою.

У випадку бінарного виявлення можлива тільки наявність чи відсутність сигналу, тобто логарифми раніше приведеної формули (8.48) для цих випадків мають вид

(8.50)

Приймач фіксує одиницю, якщо

ln P_y(1)>ln P_y(0), (8.51)

що в реальному пристрої зводиться до умови

У₁₂>U₀, (8.52)

де негативний зсув

U₀=ln(P(0)/P(1))+Э/N₀. (8.53)

У протилежному випадку вважається, що прийнято нуль.

Ймовірність помилкової тривоги в таких умовах дорівнює ймовірності виконання умови (8.52) при відсутності сигналу, тобто силами перешкоди, а імовірність пропуску зводиться до ймовірності невиконання умови (8.52), незважаючи на присутність подавленого перешкодою сигналу. Для випадків, коли припустимі ймовірності помилок не перевищують 0,1, можна користатися формулою

(8.54)

У цьому випадку надійність виявлення не залежить від форми сигналу, її визначає тільки енергія Э.

Якщо обидва сигнали ненульові, то мінімальна ймовірність помилок виходить, коли енергія цих сигналів однакова. Практично це відповідає випадкам телеграфного зв'язку з фазовою маніпуляцією х₂(t)=-x₁(t) і частотною маніпуляцією .

У випадку багатьох (m) ортогональних рівноймовірних сигналів з однаковою енергією, що не перекриваються в часі чи по частотних спектрах, переданий сигнал також виділяється серед інших своєю функцією кореляції. Для випадків, коли Р_ош <0,1, справедливе вираження

Э/N₀ ≈2ln(1/P_пом)+ln(m – 1) – 2,8. (8.55)

Поиск по сайту: