Ентропія неперервних повідомлень

Використовувані до теперішнього часу роздуми про кількість інформації явно не підходять для випадку, коли повідомлення міститься не в дискретних посиланнях, а в неперервній множині станів, т.б. коли повідомлення і відповідний йому сигнал являються неперервними функціями часу.

Оперуючи раніше встановленими закономірностями, ми в нашому випадку отримаємо нескінчену кількість інформації при кінцевій тривалості сигналу (через нескінченно велику кількість можливих його сигналів, що породжує нульову ймовірність кожного з них). Для подолання вказаної математичної трудності припускається заміна неперервного повідомлення дискретним, т.д. передача дискретної послідовності миттєвих значень в моменти часу, розділені визначеними інтервалами. Величина цих інтервалів позначається Δt, а її кількісне значення буде визначене далі теоремою відліку (Котельникова). Миттєві значення функції в реальних системах з перешкодами також не повинні мати нескінчену кількість можливостей. Достатньо передавати ці значення функції з точністю до ефективного значення перешкоди, т.б. вводячи кінцеву кількість дозволених значень (рівнів), відстань між якими визначається рівнем перешкод в каналі.

З метою застосування формули (2.7) для випадку неперервного повідомлення поняття ймовірності виражається через функцію щільності ймовірності даного розприділення станів, т.д. розглядаються ймовірності того, що значення випадкових величин виявляються в межах раніше позначених інтервалів (сукупностей чисел). Тоді вираз ентропії повідомлення з неперервним розприділенням елементів можна написати, модифікуючи формулу (2.8) для випадку дискретного розприділення:

;

. (2.15)

При зменшенні Δх (збільшенні m) перша сума в межі прямує до інтегралу:

. (2.16)

Одержана величина називається приведеною ентропією. Оскільки , друга сума рівна . Таким чином, ентропія неперервного повідомлення визначається за формулою:

. (2.17)

Інформативність повідомлення до нашого вмішування повністю зумовлена приведеною ентропією, що відображає статистику станів елементів повідомлення. Величина log₂Δx залежить тільки від вибраного інтервалу квантування Δх, який визначає точність квантування станів, і при постійному Δх являється постійною величиною.

Для визначення максимуму ентропії неперервного повідомлення слід відшукати її умовний екстремум, враховуючи додаткові умови, що накладаються на властивості повідомлення. Перше з них відоме з випадку дискретного повідомлення і зводиться до виразу:

; (2.18)

друге відноситься до практичної можливості реалізації неперервного сигналу і стверджує, що дисперсія станів елементів повідомлення — стала величина:

. (2.19)

Застосовуємо той же метод множників Лагранжа і, виходячи з рівнянь (2.16), (2.18) і (2.19), введемо позначення

; (2.20)

; (2.21)

; (2.22)

і складаємо рівняння Ейлера

. (2.23)

Визначаючи часткову похідну цього виразу по φ(х) і прирівнюючи її до нуля, здійснюємо пошук тієї густини імовірності, якій відповідає максимальна ентропія неперервного повідомлення:

;

.

Так як , то

,

або 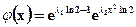. (2.24)

Постійні множники визначаємо, підставляючи одержане значення φ(х) в вираз додаткових умов

; (2.25)

. (2.26)

Згідно таблиць інтегралів [17]

.

Рівняння (2.25) і (2.26) можна переписати у вигляді

; (2.27)

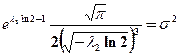; (2.28)

і, розділивши (2.27) на (2.28), встановити, що

. (2.29)

Підставляючи отримане значення в формулу (2.27), отримаємо

.

Підставляючи останній результат в вираз (2.24), записуємо

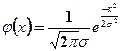. (2.30)

Останній вираз являє собою те значення функції щільності ймовірності розприділення станів, при якому ентропія повідомлень з обмеженою дисперсією максимальна. Одержана щільність ймовірностей співпадає з нормальним симетричним (гаусовим) розприділенням ймовірностей.

Отже, якщо задана дисперсія станів елементів, то повідомлення володіє найбільшою інформативністю (максимальною ентропією) в тому випадку, коли стани елементів розприділені за нормальним законом (рис.2.2.а). Якщо задана середня потужність перешкоди, то остання являється найбільш ефективною (ентропія перешкоди максимальна), коли стан утворюючих перешкоду елементів розприділений за нормальним законом. Саме цьому закону підпорядковуються амплітуди флуктуаційних шумів, а, отже, ці шуми — найбільш заважаючі із всіх можливих перешкод, так як найбільш інформативні.

φ(x) φ(x)

1/(b-a)

x x

0 0 a x₀ b

а) при заданій дисперсії станів б) при довільній дисперсії

Рисунок 2.2 – Функції щільності імовірностей, які забезпечують максимальну ентропію повідомлень:

Підставляючи одержаний результат у вираз (2.16), отримаємо

;

.

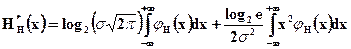Так, як , (2.31)

а , (2.32)

то 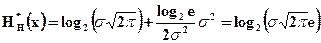, (2.33)

а повна ентропія . (2.34)

Функцію щільності ймовірностей, якій відповідає максимальна ентропія — без врахування другого обмеження (постійності дисперсії), — легко отримати, прирівнюючи другий коефіцієнт Лагранжа λ₂ нулю. Для такого випадку вираз (2.24) може бути переписаний у вигляді

. (2.35)

В цьому випадку функція щільності ймовірностей не залежить від х; отже, вона постійна на всьому інтервалі існування випадкової величини і може бути записана

. (2.36)

Отже, якщо дисперсія станів елементів не обмежена, то повідомлення володіє найбільшою інформативністю (максимальною ентропією), коли стани елементів розприділені по рівномірному закону (рис. 2.2.б).

Підставляючи вираз (2.34) в вираз (2.16), отримаємо

. (2.37)

Повна ентропія рівна . (2.38)

Порівнюючи два випадки в припущені, що кількість ентропії в повідомленнях з нормальним і рівномірним розприділеннями ймовірностей однакова, можемо вирахувати дисперсію, властиву кожному нормальному і рівномірному розподіленню з індексами “Н” і “р”. Для нормального закону розподілу отримаємо

. (2.39)

Враховуючи, що дисперсія для рівномірного закону розподілу

, (2.40)

отримаємо ;

або , (2.41)

а прирівнявши дисперсії, запишемо

. (2.42)

Отже, якщо повідомлення представлені у вигляді амплітудно-модульованих сигналів, то при однаковій їх інформативності сигнал з рівномірним розприділенням амплітуд повинен бути на 42% потужнішим.

Поиск по сайту: