Кількість інформації у всьому тексті, що передається

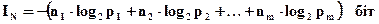. (2.7)

Таблиця 2.2–ймовірність окремих символів алфавіту джерела повідомлення

Символ (буква алфавіту)	Число символів в тексті	ймовірність символу
А Б В Г . . . Я	n1 n2 n3 n4 . . . nm	p1=n1:N p2=n2:N p3=n3:N p4=n4:N . . . pm=nm:N

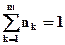
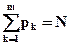
Ентропія такого повідомлення вираховується за формулою

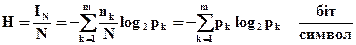. (2.8)

Як видно з формули (2.8), ентропія в цьому випадку являється істотною, обмеженою і невід'ємною величиною, так як кожен добуток загального виразу ентропії може приймати значення, обмежені можливими границями імовірності

. (2.9)

При р_к=0 значення -р_к log₂ р_к являє собою невизначеність, яка розкривається за правилом Лопіталя, т.д.

;

.

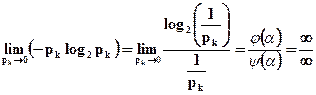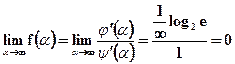При р_к=1 значення -р_к log₂ р_к також перетворюється в нуль.

Обидва ці крайні випадки можуть бути оцінені також чисто інтуїтивно. Імовірності 0 і 1 відповідно означають неможливу і повністю вірогідну подію. Таким чином, будь-яка інформація про них зайва, так як події наперед відомі.

Поведінка кожного добутку -р_к log₂ р_к між крайніми значеннями імовірності р_к може бути встановлена пошуком його екстремуму. Для цього знаходимо першу похідну добутку і прирівнюємо її до нуля.

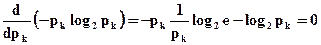. (2.10)

Звідси .

Максимальна величина одної складової буде рівна

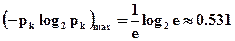, (2.11)

а поведінка цього добутку протягом всієї ділянки його існування приведена на рис. 2.1.

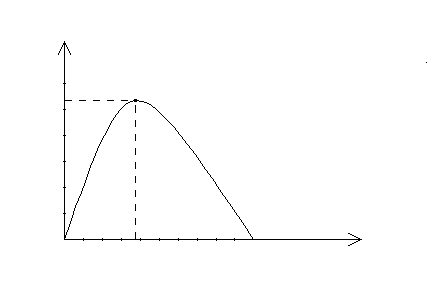
Рисунок 2.1 – Залежність -р_к log₂ р_к від ймовірності стану р_к.

Отриманий для одного добутку ентропії результат не вирішує питання про максимум ентропії повідомлення, яке містить різноймовірні символи, так як всі доданки формули (2.8) не можуть одночасно приймати значення, визначене виразом (2.11). Це неможливо, так як

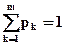. (2.12)

Для визначення максимуму ентропії дискретного повідомлення необхідно відшукати її умовний екстремум — враховуючи умову (2.12). Це можна зробити, застосовуючи метод множників Лагранжа, т.б. проводячи пошук екстремуму нової функції, утвореної у вигляді суми виразу, для якого необхідно визначити умовний екстремум, і додаткову умову, попередньо помноженого на невизначений множник Лагранжа:

;

.

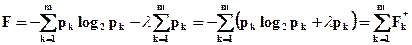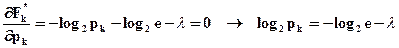На цьому етапі треба було б перейти до визначення множника λ, однак в даному випадку це зайве, так як і без того видно, що шукана величина р_к не залежить від k, отже, всі р_к рівні між собою. В результаті

. (2.13)

Одержаний вираз співпадає з рівністю (2.6), виведеною раніше для випадку, коли елементи повідомлення рівноймовірні. Таким чином, ентропія повідомлення, яка містить різноймовірні символи, завжди менша ентропії повідомлення, що складається з рівноймовірних символів. Ентропія бінарного повідомлення (m=2) завжди знаходиться в межах між 0 і 1.

Практично дискретні повідомлення (друкований текст, людська мова) звичайно мають сильно знижену ентропію, так як її, крім нерівної ймовірності символів, заважають також зв'язки (кореляція) між окремими символами (буквами, звуками). Завжди існує більша ймовірність того, що слідом за однією конкретною буквою піде друга визначена буква.

В таких випадках інформація, що буде отримана від цієї букви, буде незначна. Вказана обставина враховується поняттям надмірності, числове значення якої визначається за формулою

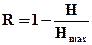. (2.14)

Будь-яка надмірність загружає канали передачі, являючись одночасно своєрідним захисником повідомлення від перешкод. Мовою без надмірності можна було б користуватись тільки в акустичній камері.

Поиск по сайту: