Покращення енергетики сигналів в системах з ЧРК

Для одержання невикривленої модуляції необхідно залишатися в межах лінійної частини відповідної модуляційної характеристики. Перевищення модулюючим коливанням деякого допустимого рівня лінійної модуляції U_ЛМ призводить до появи викривлень.

У випадку модуляції, переносчика складним сигналом викладене зводиться до потреби, щоб для амплітудної модуляції загальний коефіцієнт глибини модуляції

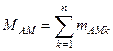, (6.14)

для фазової модуляції загальний індекс кутової модуляції

, (9.8)

а для частотної модуляції сумарна девіація кутової частоти

(9.9)

не перевищували допустимих значень. Оскільки вказані величини досягають теоретично можливого максимального значення дуже рідко, то заради цих випадків недоцільно занижувати середню глибину модуляції, так як це призводить до пониження завадостійкості. Тому перед модуляцією виконують обмеження великих викидів миттєвих значень повідомлення. Таким чином, за рахунок деякого викривлення повідомлення досягається збільшення завадостійкості зв'язку.

З метою зменшення викривлень, що викликані таким обмеженням, іноді застосовують попередній стиск, або компресію, сигналу, т.б. пропускають його через пристрій, що має амплітудну характеристику, яка змінюється за логарифмічним законом. Така дія має ту перевагу перед обмеженням сигналу, що зберігає можливість його відновлення на місці прийому. Останнє реалізується так званим експандером.

У випадку, коли несуча модулюється додаванням в свою чергу модульованих піднесучих, вказана умова відноситься до максимального миттєвого значення цієї суми, т.б.

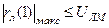. (9.10)

Виконання цієї умови дає повну гарантію відсутності викривлень, що породжується явищем перемодуляції, т.б. виходом сумарної напруги суми модульованих піднесучих за межі напруги лінійної модуляції U_ЛМ. Однак модулююча напруга досягає свого теоретично можливого максимуму в дуже рідких випадках — тільки тоді, коли вершини всіх компонентів, що входять до складу складного модулюючого коливання, співпадають. Звичайно, що невигідно, орінтуючись на згадані виключні (рідкісні) випадки, більшу частину часу працювати в режимі заниженої глибини модуляції, яка зменшує завадостійкість сигналів. Тому рівень окремих піднесучих визначається виходячи з допустимої для конкретного випадку зв'язку ймовірності перемодуляції. Математично це зводиться до наступного.

Для виключення викривлень від перемодуляції навіть в найбільш несприятливих випадках, т.б. коли глибина модуляції в усіх каналах дорівнює 100% і фази всіх каналів співпадають, однакові за своїм значенням амплітуди немодульованих піднесучих s_k0 можуть бути виражені через амплітуду стовідсотково модульованого сигналу s_kМ і кількість каналів N багатоканальної системи наступним чином:

для випадку АМ

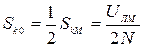, (9.11)

для випадку ЧМ

. (9.12)

Надаючи амплітудам піднесучих більші значення, можемо розраховувати ймовірність перемодуляції. Припускаючи, що фази всіх піднесучих випадкові й рівноймовірні в інтервалі від нуля до 2π, а кількість каналів достатньо велика (N≥10), зможемо з достатньо хорошим наближенням вважати, що сума миттєвих значень піднесучих (ω) розподілена за нормальним законом, т.б. густина її ймовірностей виражається формулою (2.30).

Дисперсія розглянутого нами процесу може бути виражена з врахуванням формул (4.42) та (4.44) як

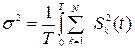, (9.13)

для випадку стовідсоткової амплітудної модуляції піднесучих її корінь набуває вигляду:

, (9.14)

а для випадку частотної модуляції

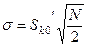. (9.15)

Позначення S_k0' введено для вибраної амплітуди піднесучої, яка в загальному випадку більша за значенням S_k0, який гарантує повну відсутність перемодуляції.

Рисунок 9.9 – Графік функції густини ймовірностей

суми модульованих піднесучих

Маючи вираз функції густини ймовірностей суми модульованих піднесучих, можемо знайти ймовірність перемодуляції, т.б. ймовірність того, що сума піднесучих вийде за межі U_ЛМ. Ця ймовірність на рис. 9.9 зображена заштрихованою площиною і визначається виразом

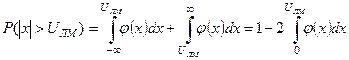. (9.16)

Підставляючи в цю рівність значення φ(х) з формули (2.30), отримаємо

. (9.17)

Вводячи нове позначення

(9.18)

і здійснюючи випливаючу з цього заміну змінних, в ході якої позначаємо

, (9.19)

вираз (9.17) переписуємо у вигляді

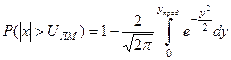. (9.20)

Так як частина правої сторони останнього рівняння, а саме

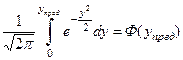, (9.21)

є функцією Лапласа або інтегралом ймовірностей помилок, значення якого протабульовані, то

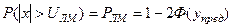(9.22)

а, отже, можна визначити черговість знаходження значення амплітуди кожної піднесучої багатоканального повідомлення виходячи з допустимої ймовірності перемодуляції.

В першу чергу по заданому P(|x|>U_ЛМ) визначається відповідне у_пред. Для цього потрібно користуватися таблицями функції Лапласа і формулою (9.22). В таблиці 9.2 приведені деякі результати такого розрахунку.

Таблиця 9.2 – Результати розрахунку

Підставляючи у вираз (9.19) значення U_ЛМ та σ, одержані з формул (9.11), (9.12), (9.14) та(9.15), визначаємо допустимі збільшення амплітуди піднесучих:

(9.23)

та

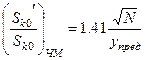. (9.24)

Використання приведених співвідношень дає можливість за рахунок незначних допустимих викривлень збільшити потужність сигналів в каналах багатоканального тракту, що, в свою чергу, сприяє завадостійкості всіх повідомлень, що передаються по цим каналам.

Поиск по сайту: