АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Длина тел в разных системах отсчёта

Читайте также:
  1. А) процесс выделения на электродах веществ, входящих в состав электролита Б) объединение ионов разных
  2. Агрегатный индекс цен: особенности построения с учетом разных весов
  3. Адгезия – притяжение частиц из разных фаз.
  4. Арифметические действия в двоичной и шестнадцатеричной системах счисления
  5. Борьба с биологическим обрастанием, коррозией и отложениями в системах оборотного водообеспечения
  6. В разных категориях тяжести и напряженности, дБА
  7. Ваш муж может быть не алкоголиком (тяжелым пьяницей), тип №1 или алкоголиком на разных этапах прогрессирования алкоголизма, тип №2, №3 и №4
  8. Взаємодії в екологічних системах. Принципи формування екосистем
  9. Викривлення в системах з ВРК
  10. Викривлення в системах з ЧРК
  11. Выполнение арифметических операций в позиционных системах счисления
  12. Вычисление скалярного произведения векторов через их координаты. Длина вектора. Угол между векторами.

Длина стержня в системе К’:

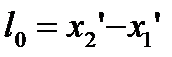
Длина стержня в системе К:

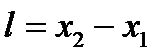
Из преобразований Лоренца:

,

т.о.: .

Линейный размер тела, движущегося относительно инерциальной системы отсчёта уменьшается в направлении движения в - это Лоренцево сокращение длины. Поперечные размеры не зависят от скорости движения и одинаковы во всех системах отсчёта.

Линейные размеры тела наибольшие в той инерциальной системе отсчёта, отн-но которой тело покоится.

 

35. Длительность событий в разных системах отсчёта.

Пусть в некоторой точке (с координатой х), покояшейся относительно системы К, происходит событие, длительность которого

,где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К: ,

причём началу и концу события, согласно преобраз-ям Лоренца, соответствуют:

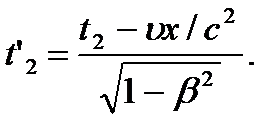
Прдставляя второе в первое получим:

.

Отсюда видно, что , т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчёта, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчёта, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчёта, относительно которой часы движутся. Из . следует, что замедление хода часов становиться заметным лишь при скоростях, близких к скорости света в вакууме.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)