Кинетическая энергия вращения

13. Механическая энергия. Закон сохранения механической энергии.

Полная механическая энергия системы – энергия механического движения и взаимодействия: Е=Т+П, т.е. равна сумме кинетической и потенциальной энергий.

Пусть F₁’…F_n’ – равнодействующие внутренних консервативных сил. F₁…F_n - равнодействующие внешних консервативных сил. f₁…f_n. Запишем уравнения 2зН для этих точек:

Умножим каждое ур-е на , учтя, что .

Сложим ур-я:

Первый член левой части:

Где dT есть приращение кинетической энергии системы.

Второй член равен элементарной работе внутренних и внешних сил, взятой со знаком минус, т.е. равен элементарному приращению потенциальной энергии dП системы.

Правая часть равенства задаёт работу вешних неконсервативных сил, действующих на систему. Т.о.:

.Если внешние неконсервативные силы отсутствуют, то:

d(Т+П)=0;Т+П=Е=const

Т.е. полная механическая энергия системы сохраняется постоянной. Закон сохранения механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.

14. Абсолютно упругий удар.

Удар (соударение) – столкновение 2-х или более тел, при котором взаимодействие длится очень короткое время. При ударе внешними силами можно пренебречь.

Коэффициент восстановления – отношение нормальной составляющей относительной скорости тел после и до удара.

, если для сталкивающих тел =0, то такие тела называются абсолютно неупругими, если =1 то абсолютно упругими.

Линия удара – прямая проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения.

Центральный удар – такой удар, при котором тела до удара движутся вдоль прямой, проходящей через их центр масс.

Абсолютно упругий удар – столкновение 2-х тел, в результате которого в обоих взаимодействующих не остаётся ни каких деформаций и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию.

Для абсолютно упругого удара выполняются закон сохранения импульса и закон сохранения энергии.

Законы сохранения:

m₁v₁+m₂v₂=m₁v’₁+m₂v’₂

после преобразований:

откуда:v₁+v₁’=v₂+v₂’

решая последнее ур-е и предпедпоследнее найдём:

15. Абсолютно неупругий удар.

Удар (соударение) – столкновение 2-х или более тел, при котором взаимодействие длится очень короткое время. При ударе внешними силами можно пренебречь.

Коэффициент восстановления – отношение нормальной составляющей относительной скорости тел после и до удара.

, если для сталкивающих тел =0, то такие тела называются абсолютно неупругими, если =1 то абсолютно упругими.

Линия удара – прямая проходящая через точку соприкосновения тел и нормальная к поверхности их соприкосновения.

Центральный удар – такой удар, при котором тела до удара движутся вдоль прямой, проходящей через их центр масс.

Абсолютно неупругий удар – столкновении 2-х тел, в результате которого тела объединяются, двигаясь дальше, как единое целое.

Закон сохранения импульса:

отсюда:

Если шары двигались навстречу друг другу, то при абсолютно неупругом ударе шары движутся в сторону большего импульса.

16. Поле тяготения, напряжённость, потенциал.

Закон всемирного тяготения: между любыми двумя мт действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек и обратно пропорциональная квадрату расстояния между ними:

G – Гравитационная постоянная (G=6,67*10^-11Hm²/(кг)²)

Гравитационное взаимодействие между двумя телами осуществляется с помощью поля тяготения, или гравитационного поля. Это поле порождается телами и является формой существования материи. Основное св-во поля в том, что на всякое тело внесённое в это поле действует сила тяготения:

Вектор не завит от массы и называется напряжённостью поля тяготения.

Напряжённость поля тяготения определяется силой действующей со стороны поля на мт единичной массы, и совпадает по направлению с действующей силой, напряжённость есть силовая хар-ка поля тяготения.

Поле тяготения однородное если напряжённость во всех точках его одинакова, и центральным, если во всех точках поля векторы напряжённости направлены вдоль прямых, которые пересекаются в одной точке.

Гравитационное поле тяготения – носитель энергии.

На расстоянии R на тело действует сила:

при перемещении этого тела на расстояние dR затрачивается работа:

Знак минус появляется, т.к. сила и перемещение в данном случае противоположны по направлению.

Затраченная работа в пол тяготения не зависит от траектории перемещения, т.е. илы тяготения консервативны, а поле тяготения является потенциальным.

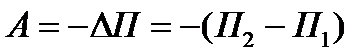
Если то П₂=0, тогда запишем: ,

Потенциал поля тяготения – скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля или работой по перемещению единичной массы из данной точки поля в бесконечность. Т.о.:

Эквипотенциальные – такие поверхности, для которых потенциал постоянен.

Взаимосвязь между потенциалом и напряженностью.

Знак мину указывает на то, что вектор напряжённости направлен в сторону убывания потенциала.

Если тело находится на высоте h, то

17. Неинерциальная система отсчёта. Силы инерции при ускоренном поступательном движении системы отсчёта.

Неинерциальная – система отсчёта, движущаяся относительно инерциальной системы отсчёта с ускорением.

Законы Н можно применять в неинерциальной системе отсчёта, если учесть силы инерции. Силы инерции при этом должны быть такими, чтобы вместе с силами , обусловленными воздействием тел друг на друга, они сообщали телу ускорение , каким оно обладает в неинерциальных системах отсчёта, т.е.:

; .

Силы инерции при ускоренном поступательном движении системы отсчёта.

Пусть диск равномерно вращается с угловой скоростью вокруг вертикальной оси, проходящей через его центр. На диске на разных расстояниях от оси вращения установлены маятники (на нитях подвешены шарики). При вращении маятников вместе с диском шарики отклоняются от вертикали на некоторый угол.

В инерциальной системе отсчёта, связанной с помещением, на шарик действует сила, равная , и направлена перпендикулярно оси вращения диска. Она является равнодействующей силы тяжести и силы натяжения нити :

.

Когда движение шарика установится, то:

; ,

т.е. углы отклонения нитей маятников будут тем больше, чем больше расстояние R от шарика до оси вращения диска и чем больше угловая скорость вращения .

Относительно системы отсчёта, связанной с вращающимся диском, шарик покоится, что возможно, если сила уравновешивается равной и противоположно направленной ей силой .

Сила , называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна: .

19. Гидростатическое давление, закон Архимеда, закон неразрывности струи.

Гидроаэромеханика – раздел механики, изучающий равновесие и движение жидкостей и газов, их взаимодействие между собой и обтекаемыми ими твёрдыми телами.

Несжимаемая жидкость – жидкость, плотность которой всюду одинакова и не изменяется со временем.

Давление – физическая величина, определяемая нормальной силой, действующей о стороны жидкости на единицу площади:

Закон Паскаля – давление в любом месте покоящейся жидкости одинаково по всем направлениям, причём давление одинаково передаётся по всему объёму, занятому покоящейся жидкости.

Если жидкость не сжимаема, то при поперечном сечении S столба жидкости, его высоте h и плотности вес:

А давление на нижнее основание: ,т.е. давление изменяется линейно с высотой. Давление называется гидростатическим давлением.

Из этого следует, что давление на нижние слои жидкости будет больше, чем на верхние, значит на тело, погружённое в жидкость действует выталкивающая сила, определяемая законом Архимеда: на тело погружённое в жидкость (газ), действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости: ,

Течение – движение жидкости. Поток – совокупность частиц движущейся жидкости. Линии тока – графическое изображение движения жидкости.

Течение жидкости установившееся (стационарно), если форма расположения линий тока, а так же значения скоростей в каждой её точке со временем не изменяются.

За 1с через сечение S₁ пройдёт объём жидкости равный , а через S₂ - , здесь предполагается, что скорость жидкости в сечении постоянна. Если жидкость не сжимаема, то через оба сечения пройдёт равный объём:

Это и есть уравнение неразрывности струи для несжимаемой жидкости.

20. Закон Бернулли.

Жидкость идеальна, движение стационарно.

За малый промежуток времени жидкость перемещается от сечений S₁ и S₂ к сечениям S’₁ и S’₂.

По закону сохранения энергии изменение полной энергии идеальной несжимаемой жидкости равно работе внешних сил по перемещению массы жидкости: ,

где Е₁ и Е₂ – полные энергии жидкости массой m в местах сечений S₁ и S₂ соответственно.

С другой стороны А – это работа, совершаемая при перемещении всей жидкости, заключённой между сечениями S₁ и S₂, за рассматриваемый промежуток времени . Для переноса массы m от S₁ до S’₁ жидкость должна переместится на расстояние и от S₂ до S’₂ на расстояние . ,где F₁=p₁S₁ и F₂=-p₂S₂.

Полные энергии Е₁ и Е₂ будут складываться из кинетической и потенциальной энергий массы жидкости:

Получим:

Учтя, что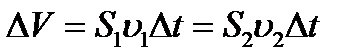

разделим ур-е на :

,

т.к. сечения выбирались произвольно, то:

Это выражение и есть уравнение Бернулли – выражение закона сохранения энергии, применительно к установившемуся течению идеальной жидкости.

p – это статическое (избыточное) давление,

- динамическое давление.

- гидростатическое давление.

Из ур-я Бернулли и ур-я неразрывности следует, что при течении жидкости по горизонтальной трубе, имеющей различные сечения, скорость жидкости больше в местах сужения, а статическое давление больше в более широких местах.

Поиск по сайту: