 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Внутренняя энергия идеального газа
Внутреннюю энергию 
газа определяют как сумму кинетической энергии теплового движения молекул и потенциальной энергии межмолекулярного взаимодействия.
Получим выражение для внутренней энергии идеального газа. В идеальном газе пренебрегают силами межмолекулярного взаимодействия. Поэтому внутренняя энергия идеального газа равна кинетической энергии его молекул.
Расчет дает, что средняя кинетическая энергия молекул
(16.1)
где 
— температура газа; 
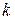— постоянная Больцмана
(
где NA — число Авогадро — число молекул в одном моле газа);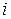 
— число степеней свободы — число независимых координат, с помощью которых может быть задано положение молекул в пространстве. Для определения положения в пространстве одноатомной молекулы достаточно трех координат 
. Следовательно, для одноатомной молекулы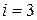 
. Для определения положения в пространстве двухатомной молекулы достаточно трех координат центра молекулы и двух значений углов φ и υ, фиксирующих направление оси молекулы. Следовательно, для двухатомной молекулы 
. Для определения положения трехатомной и более молекулы в пространстве достаточно трех координат центра молекулы и трех значений углов φ, υ и ψ, фиксирующих направление оси молекулы. Следовательно, для трехатомной и многоатомной молекулы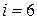 
.
Пусть в сосуде находится N молекул идеального газа. Тогда с учетом выражения (16.1) внутренняя энергия идеального газа
 |
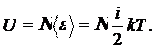(16.2)
Учитывая, что
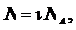
можем написать
 |
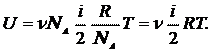(16.3)
Отметим, что внутренняя энергия является функцией состояния. Это означает, например, что при переходе газа из состояния 1 (с температурой 
) в состояние 2 (с температурой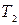 
) приращение внутренней энергии 
, т. е. не зависит от способа перехода газа из состояния 1 в состояния 2, а определяется только разностью значений внутренней энергии газа в состояния 1 и 2.
Пример 16.1. Водород, находящийся при нормальных условиях в закрытом сосуде объемом V = 5 л, охладили на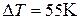 
. Найти приращение внутренней энергии газа.
Дано:
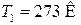V = 5 л
| Решение
 >  .
 .
|
|
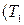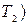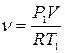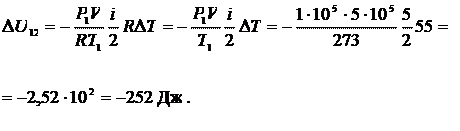
Ответ: 
Пример 16.2. Водород занимает объем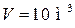 
при давлении 
Его нагрели при постоянном объеме до давления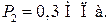 
Определить приращение 
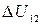внутренней энергии газа.
Дано:
 
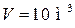
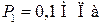
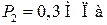
| Решение
|
|
|
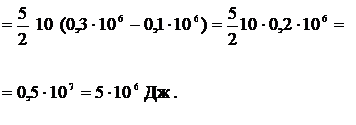
Ответ: 
Поиск по сайту: