Электроемкость плоского конденсатора

Найдем электроемкость плоского конденсатора. Плоский конденсатор состоит из двух параллельных металлических пластин (обкладок) площадью S каждая, расположенных на близком расстоянии d одна от другой. Заряды пластин + q и – q. Пространство между пластинами заполнено средой с диэлектрической проницаемостью ε (рис. 41.1).

Рис. 41.1

Для нахождения разности потенциалов Δφ между пластинами конденсатора воспользуемся соотношением (36.7). Получим выражение для напряженности E электрического поля в конденсаторе. Возьмем любую точку между пластинами конденсатора. Вследствие симметрии (заряд каждой пластины равномерно распределяется по поверхности пластины (см. пример 33.1)) вектор поля, создаваемого левой пластиной, в этой точке направлен по оси x. Определим модуль (длину) этого вектора. Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде симметричного относительно левой пластины цилиндра так, чтобы точка находилась на основании цилиндра (рис. 41.1). Найдем поток вектора сквозь гауссову поверхность:

(41.1)

где S _осн — площадь основания цилиндра. При интегрировании мы учли, что поток вектора сквозь боковую поверхность цилиндра равен нулю (линии вектора не пронизывают эту поверхность) и для всех точек основания цилиндра α = 0 и D ₁ = const.

Согласно теореме Гаусса

(41.2)

где 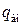— заряд пластины, сосредоточенный внутри цилиндра. Можем написать

(41.3)

(мы учли, что поверхностная плотность заряда где q и S — заряд и площадь пластины).

Подставляя выражения (41.1) и (41.3) в соотношение (41.2), получаем

откуда

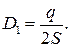(41.4)

Аналогично можно определить модуль вектора в той же точке электрического поля, создаваемого правой пластиной. Расчет дает

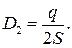(41.5)

Очевидно, внутри конденсатора

(41.6)

Воспользовавшись соотношением (39.8), находим напряженность E:

(41.7)

Подставим выражение (41.7) в соотношение (36.7) и проинтегрируем:

(41.8)

Подставляя формулу (41.8) в выражение (40.5), получаем электроемкость плоского конденсатора

(41.9)

Поиск по сайту: