 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Потенциал поля
Работа сил электростатического поля при перемещении точечного заряда 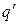 из точки 1 в точку 2
из точки 1 в точку 2
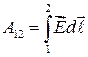 (35.1)
(35.1)
не зависит от траектории перемещения заряда 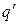 , а зависит только от положения точек 1 и 2. Следовательно, электростатическое поле является потенциальным. Можем написать
, а зависит только от положения точек 1 и 2. Следовательно, электростатическое поле является потенциальным. Можем написать
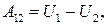 (35.2)
(35.2)
где  — убыль потенциальной энергии поля при переходе из точки 1 в точку 2.
— убыль потенциальной энергии поля при переходе из точки 1 в точку 2.
Введем скалярную величину
 (35.3)
(35.3)
и назовем ее потенциалом электрического поля. Потенциал φ равен потенциальной энергии единичного положительного точечного заряда в данной точке поля. Единицей измерения потенциала является вольт (В).
Подставляя выражение 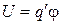 в соотношение (35.2), получаем
в соотношение (35.2), получаем
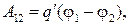 (35.4)
(35.4)
где 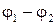 — убыль потенциала электрического поля при переходе из точки 1 в точку 2.
— убыль потенциала электрического поля при переходе из точки 1 в точку 2.
С учетом выражения (35.4) запишем соотношение (35.1) в виде
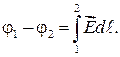 (35.5)
(35.5)
Формула (35.5) дает возможность найти потенциал любого электростатического поля. Найдем потенциал поля точечного заряда q. Так как  где
где 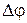 — приращение потенциала, имеем для элементарного перемещения
— приращение потенциала, имеем для элементарного перемещения 
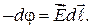 (35.6)
(35.6)
С учетом выражения (31.3) можем написать
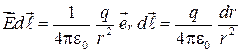 (35.7)
(35.7)
(мы учли, что скалярное произведение 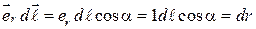 — элементарному приращению модуля радиуса-вектора (рис. 35.1)).
— элементарному приращению модуля радиуса-вектора (рис. 35.1)).

Рис. 35.1
Подставим выражение (35.7) в соотношение (35.6) и проинтегрируем:


 (35.8)
(35.8)
(при интегрировании мы приняли φ = 0 при r = ∞). Из выражения (35.8) видно, что в зависимости от знака заряда q, потенциал φ может быть как положительным, так и отрицательным.
Найдем потенциал поля системы N точечных зарядов 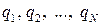 . Используя принцип суперпозиции электрических полей, можем написать
. Используя принцип суперпозиции электрических полей, можем написать
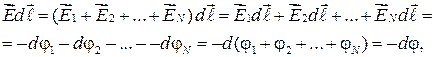
откуда
 (35.9)
(35.9)
где 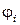 — потенциал поля в интересующей нас точке, создаваемый i -м точечным зарядом в отсутствие других точечных зарядов. Следовательно, принцип суперпозиции справедлив и для потенциала электрического поля.
— потенциал поля в интересующей нас точке, создаваемый i -м точечным зарядом в отсутствие других точечных зарядов. Следовательно, принцип суперпозиции справедлив и для потенциала электрического поля.
Пример 35.1. Заряженная частица, пройдя ускоряющую разность потенциалов 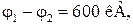 приобрела скорость
приобрела скорость  Найти удельный заряд частицы (отношение ее заряда q к массе m).
Найти удельный заряд частицы (отношение ее заряда q к массе m).
Дано:
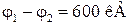
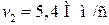
| Решение

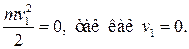
|
| q/m –? |


Ответ: 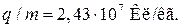
§ 36. Связь между φ и 
Пусть перемещение  параллельно оси x. В этом случае
параллельно оси x. В этом случае
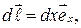
где dx — элементарное приращение координаты x. Можем написать
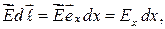
где Ex — проекция вектора  на ось x. Учитывая выражение (35.6), получаем
на ось x. Учитывая выражение (35.6), получаем
 (36.1)
(36.1)
где символ частной производной подчеркивает, что функцию 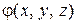 надо дифференцировать только по x, считая y и z при этом постоянными. Аналогично получаем
надо дифференцировать только по x, считая y и z при этом постоянными. Аналогично получаем
 (36.2)
(36.2)
 (36.3)
(36.3)
Сам вектор
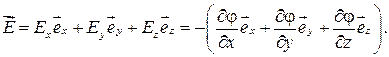 (36.4)
(36.4)
Выражение в скобках есть градиент потенциала φ (grad φ). Следовательно,
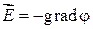 (36.5)
(36.5)
— напряженность  поля равна со знаком минус градиенту потенциала φ этого поля.
поля равна со знаком минус градиенту потенциала φ этого поля.
Пример 36.1. Имеем бесконечную равномерно заряженную плоскость с поверхностной плоскостью σ. Определить потенциал φ электрического поля на расстоянии x от плоскости.
| Дано: σ x | Решение Для нахождения потенциала φ воспользуемся соотношением (36.5) и результатом примера 33.1. Можем написать |
| φ –? |
 (36.6)
(36.6)
откуда
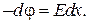 (36.7)
(36.7)
Подставим выражение (33.5) в соотношение (36.7) и проинтегрируем:
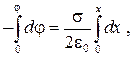
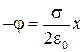
или
 (36.8)
(36.8)
(при интегрировании мы приняли φ = 0 при x = 0).
Графически зависимость φ(x) электрического поля равномерно заряженной бесконечной плоскости представлена на рис. 36.1.
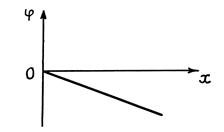
Рис. 36.1
Пример 36.2. Имеем равномерно заряженную сферу с поверхностной плотностью заряда σ. Радиус сферы R. Определить потенциал φ электрического поля на расстоянии r от центра сферы.
| Дано: σ R r | Решение Для нахождения потенциала φ воспользуемся соотношением (36.5) и результатом примера 33.2. Можем написать |
| φ –? |
 (36.9)
(36.9)
где  — единичный вектор радиуса-вектора
— единичный вектор радиуса-вектора  , проведенного из центра сферы, помещенного в начало координат, до интересующей нас точки поля. Из соотношения (36.9) следует
, проведенного из центра сферы, помещенного в начало координат, до интересующей нас точки поля. Из соотношения (36.9) следует
 (36.10)
(36.10)
Так как внутри сферы (r < R) Е = const, согласно соотношению (36.10)
 (36.11)
(36.11)
Следовательно, потенциал φ поля во всех точках внутри сферы одинаков.
Определим φ в точке, находящейся вне заряженной сферы (r > R). Подставим выражение (33.9) в соотношение (36.10) и проинтегрируем:
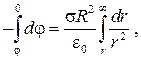
 (36.12)
(36.12)
(при интегрировании мы приняли φ = 0 при r = ∞). Следовательно, потенциал φ поля вне заряженной сферы убывает с расстоянием r. На поверхности сферы (r = R), а также во всех точках внутри сферы
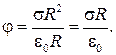 (36.13)
(36.13)
Графически зависимость φ(r) электрического поля равномерно заряженной сферы представлена на рис. 36.2.
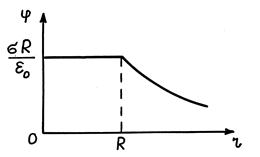
Рис. 36.2
Пример 36.3. Имеем равномерно заряженный шар с объемной плотностью заряда ρ. Радиус сферы R. Определить потенциал φ электрического поля на расстоянии r от центра шара.
| Дано: ρ R r | Решение Для нахождения потенциала φ воспользуемся соотношением (36.5) и результатом решения примера 33.3. Можем написать |
| φ –? |
 (36.14)
(36.14)
где  — единичный вектор радиуса-вектора
— единичный вектор радиуса-вектора  , проведенного из центра шара, помещенного в начало координат, до интересующей нас точки поля. Из соотношения (36.14) следует
, проведенного из центра шара, помещенного в начало координат, до интересующей нас точки поля. Из соотношения (36.14) следует
 (36.15)
(36.15)
Сначала определим φ в точке, находящейся внутри заряженного шара (r < R). Подставим выражение (33.14) в соотношение (36.15) и проинтегрируем:
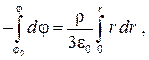

откуда
 (36.16)
(36.16)
где  — потенциал в центре шара. Следовательно, потенциал φ поля внутри заряженного шара убывает с расстоянием r.
— потенциал в центре шара. Следовательно, потенциал φ поля внутри заряженного шара убывает с расстоянием r.
Теперь определим φ в точке, находящейся вне заряженного шара (r > R). Подставим выражение (33.15) в соотношение (36.15) и проинтегрируем:

 (36.17)
(36.17)
(при интегрировании мы приняли φ = 0 при r = ∞). Следовательно, потенциал φ поля вне заряженного шара убывает с расстоянием r.
На поверхности шара (r = R)
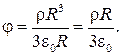 (36.18)
(36.18)
Записав выражение (36.16) для поверхности шара

найдем потенциал  в центре шара:
в центре шара:
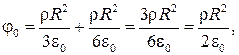 (36.19)
(36.19)
откуда получаем окончательное выражение для φ в точке, находящейся в центре шара:
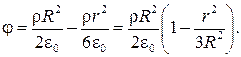 (36.20)
(36.20)
Графически зависимость φ(r) электрического поля равномерно заряженного шара представлена на рис. 36.3.

Рис. 36.3
Поиск по сайту: