Путь и перемещение

Подписано в печать 18.05.99. Формат 60x90 1/8

Объем 20,8 уч.-изд.л. Заказ №1319. Тираж 2500 экз.

Отпечатано в Орехово-Зуевской типографии:

г. Орехово-Зуево, Моск. обл., ул. Дзержинского, д. 1.

МЕХАНИКА

ГЛАВА 1. КИНЕМАТИКА И ДИНАМИКА ЧАСТИЦЫ

Путь и перемещение

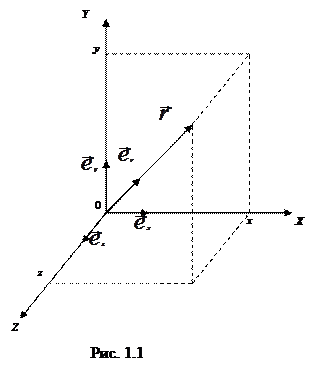Механика — это раздел физики, в котором изучают механическое движение — изменение положения тела в пространстве с течением времени. Положение тела в пространстве определяют по отношению к другому телу, с которым связывают систему координат, например, декартову, представляющую собой три взаимно перпендикулярные оси x, y, z (рис. 1.1). Система координат плюс часы для отсчета времени образуют систему отсчета.

Рассмотрим кинематику движения тела, т. е. движение без учета его причины. Размерами движущегося тела будем пренебрегать и называть его просто частицей.

Положение тела (частицы) в любой момент времени 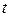можно задать с помощью радиуса-вектора ,проведенного из начала координат 0 в точку пространства, в котором находится тело в момент времени 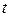(рис. 1.1). Из рис. 1.1 видно, что радиус-вектор можно записать в виде

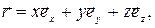(1.1)

где 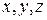— координаты точки пространства, , 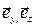— орты системы координат — единичные по модулю безразмерные векторы, направленные по осям 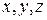соответственно.

Длина радиуса-вектора (его модуль)

(1.2)

Очевидно, при движении частицы ее радиус-вектор меняется в общем случае как по модулю, так и по направлению, т. е. радиус-вектор зависит от времени :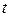

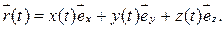(1.3)

Если известна зависимость 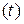, говорят, что задан закон движения частицы.

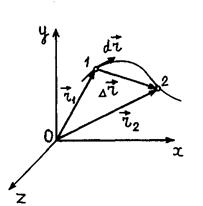
Линию, описываемую частицей при ее движении, называют траекторией частицы (рис. 1.2). Пусть за промежуток времени 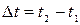частица переместилась вдоль траектории из точки 1 в точку 2 (рис. 1.2) Проведем из точки 1 в точку 2 вектор 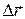и назовем его перемещением частицы за промежуток времени 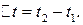Из рис. 1.2 видно, что

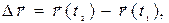(1.4)

приращению радиуса-вектора частицы за промежуток времени .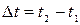

С учетом выражения (1.1) можем написать

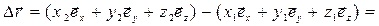
(1.5)

Элементарное перемещение частицы из точки 1 за элементарный (очень малый) промежуток времени

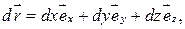(1.6)

причем нетрудно видеть, что вектор 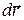направлен по касательной к траектории в точке 1.

Назовем длину отрезка траектории между точками 1 и 2 путем S , пройденным частицей за промежуток времени Из рис. 1.2 видно, что обычно путь больше длины (модуля) перемещения. Однако по мере уменьшения пути это различие уменьшается. Для элементарного (очень малого) пути 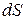оно становиться ничтожным, что дает право написать

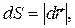
(1.7)

где 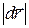— модуль элементарного перемещения частицы.

Поиск по сайту: