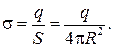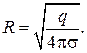Напряженность поля

Экспериментально было обнаружено, что частицы могут испытывать взаимодействие гораздо более сильное, чем гравитационное. Для объяснения этого к массе m частицы добавили еще одну характеристику частицы — электрический заряд q, измеряемый в кулонах (Кл).

Назовем заряженную частицу, т. е. частицу, имеющую заряд q, точечным зарядом q (в отличие от заряженного тела, размерами которого нельзя пренебречь в условиях данной задачи). Каждый неподвижный точечный заряд q создает в окружающем пространстве электрическое поле (точнее электростатическое поле). На любой другой точечный заряд 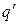в этом поле будет действовать электрическая сила

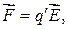(31.1)

где вектор называют напряженностью электрического поля в точке, где находится заряд 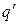. Сила 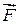может быть направлена или к заряду q, или от него. В связи с этим ввели два вида заряда: положительный и отрицательный. Разноименные заряды притягиваются, а одноименные — отталкиваются друг от друга (рис. 31.1).

Рис. 31.1

Напряженность определяют как силу, действующую на единичный положительный точечный заряд в данной точке поля:

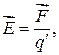(31.2)

где 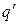> 0. Из выражения (31.2) видно, что размерность есть ньютон на кулон (Н/Кл).

Опыт показывает, что подвижный точечный заряд q создает на расстоянии r от него напряженность

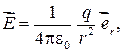(31.3)

где ε₀ — электрическая постоянная (ε₀ = 8,85·10^–12 Кл²/(Н·м²)); 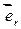— единичный вектор радиуса-вектора , проведенного от центра поля, помещенного в начало координат, в котором расположен точечный заряд q, до интересующей нас точки поля.

Из выражения (31.1) видно, что электрическая сила 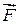, действующая на заряд 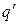, направлена так же, как и вектор , если заряд 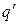положительный, и противоположно вектору , если заряд 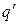отрицательный (рис. 31.2).

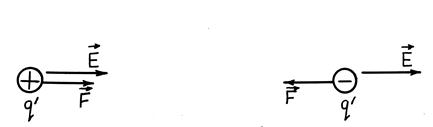
Рис. 31.2

Из опыта следует, что напряженность поля системы N неподвижных точечных зарядов

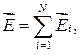(31.4)

где — напряженность поля в интересующей нас точке, создаваемая i -м точечным зарядом в отсутствие других точечных зарядов. Соотношение (31.4) выражает принцип суперпозиции электрических полей.

Пример 31.1. Два шарика с массами по 0,3 кг находятся на таком расстоянии, что взаимодействие их зарядов уравновешивается силой гравитационного притяжения. Найти радиусы шаров, если поверхностная плотность заряда шаров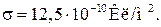

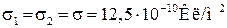
Дано:   m 1 = m 2 = m =0,3 кг F э = F гр   R 1 = R 2 = R	Решение     . F э = F гр.   .
R –?

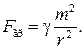
Ответ: R = 4 см.

Пример 31.2. Точечные заряды q ₁ = 2 q и q ₂ = – q расположены, как показано на рис. 31.4. Расстояние между зарядами равно d. Определить, на каком расстоянии x ₁ от заряда q ₁ напряженность электрического поля равна нулю.

Дано:   q 1 = 2 q   q 2 = – q   d E(x 1) = 0	Решение 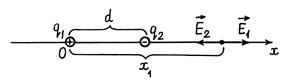  Рис. 31.3
x 1 –?

Согласно принципу суперпозиции электрических полей в точке, где должно выполняться условие

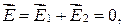
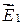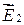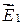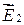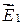где и — напряженности полей, создаваемых зарядами q ₁ и q ₂ в этой точке. Очевидно, это условие выполняться не будет вне оси x (векторы и направлены под углом друг к другу), а также на оси x слева от заряда q ₁, где всегда E ₁ > E ₂ (см. формулу (31.3) и условие задачи). Между зарядами на оси x не может равняться нулю, так как векторы и 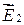направлены в одну сторону. Остается предположить, что искомая точка лежит на оси x справа от заряда q ₂ (см. рис. 31.3). Расстояние x ₁ от заряда q ₁ найдем из условия

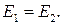
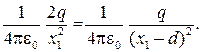
Сократим на и извлечем корень квадратный из левой и правой частей равенства

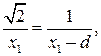
откуда

Ответ: x ₁ = 3,5 d.

§ 32. Поток вектора

Наглядно поле вектора изображают с помощью линий вектора , которые проводят следующим образом:

1) касательная к ним в каждой точке совпадает с направлением вектора ;

2) число линий, пронизывающих единицу площади поверхности, перпендикулярную линиям (густота линий), равно модулю вектора (рис. 32.1).

Электрическое поле называют однородным, если в каждой точке поля вектор = const. Линии вектора такого поля параллельны и расстояния между ними одинаковы (рис. 32.2).

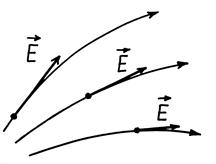
Рис. 32.1 Рис. 32.2

Линии вектора электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах.

Возьмем элементарную площадку dS в поле вектора (рис. 32.3). Пусть 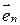— единичный вектор нормали к площадке dS, α — угол между векторам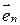и и . Тогда число линий вектора , пронизывающих dS, равно

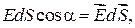
где — вектор, модуль которого равен dS, а направление совпадает с единичным вектором 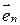нормали к площадке dS.

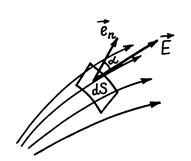
Рис. 32.3

Назовем потоком Ф вектора сквозь произвольную поверхность S число линий вектора , пронизывающих эту поверхность. Очевидно,

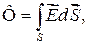
интегралу по поверхности S от скалярного произведения векторов и 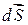. Поток — величина алгебраическая. Знак потока зависит от выбора направления нормали к dS. Для замкнутых поверхностей принято брать внешнюю нормаль.

§ 33. Теорема Гаусса для поля вектора

Теорема. Поток вектора сквозь любую замкнутую поверхность S равен q _вн/ε₀, где q _вн — алгебраическая сумма зарядов внутри этой поверхности:

(33.1)

где кружок у интеграла означает, что интегрирование проводится по замкнутой поверхности.

Доказательство теоремы. Рассмотрим электрическое поле одного неподвижного точечного заряда q. Пусть q > 0. Мысленно окружим заряд q произвольной замкнутой поверхностью S (рис. 33.1).

Рис. 33.1

Найдем поток d Ф вектора сквозь элемент dS поверхности. Очевидно,

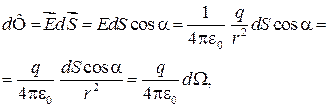
где — элементарный телесный (пространственный) угол внутри конуса, опирающегося на dS, с вершиной в точке расположения заряда q.

Поток вектора сквозь всю замкнутую поверхность S

где 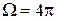— полный телесный угол. Мы получили

что совпадает с выражением (33.1).

Теперь рассмотрим электрическое поле, создаваемое системой N неподвижных точечных зарядов 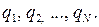Мысленно окружим эту систему зарядов произвольной замкнутой поверхностью S. Используя принцип суперпозиции электрических полей, можем написать

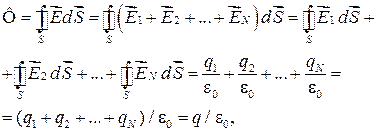
где q — алгебраическая сумма N зарядов, что совпадает с выражением (33.1).

Теорема Гаусса позволяет в некоторых случаях очень просто определить напряженность в любой точке электрического поля.

Пример 33.1. Имеем бесконечную равномерно заряженную плоскость с поверхностной плотностью заряда σ. Определить напряженн о сть Е электрического поля на расстоянии x от плоскости.

Дано:   σ   x	Решение   Проведем ось x, как показано на рис. 33.2 (перпендикулярно плоскости слева направо). Пусть плоскость заряжена положительно. Вследствие симметрии вектор поля, создаваемого плоскостью, в интересующей нас точке направлен по оси x. Определим модуль (длину) этого вектора.
E –?

Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде симметричного относительно плоскости цилиндра так, чтобы точка находилась на основании цилиндра (рис. 32.2). Найдем поток вектора сквозь гауссову поверхность:

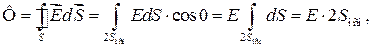(33.2)

где S _осн — площадь основания цилиндра. При интегрировании мы учли, что поток вектора сквозь боковую поверхность цилиндра равен нулю (линии вектора не пронизывают эту поверхность) и для всех точек основания цилиндра α = 0 и Е = const.

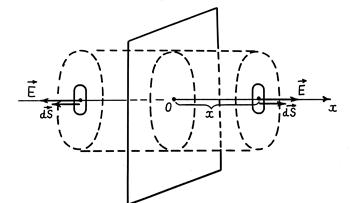
Рис. 33.2

Согласно теореме Гаусса

(33.3)

где — заряд плоскости, сосредоточенный внутри цилиндра. Найдем его. По определению, поверхностная плотность заряда

В случае равномерно заряженной плоскости (σ = const) можем написать

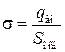
(из рис. 33.2 видно, что заряд 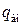сосредоточен на части плоскости с площадью S _осн), откуда

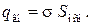(33.4)

Подставляя выражения (33.2) и (33.4) в соотношение (33.3), получаем

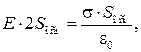
откуда

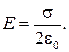(33.5)

Из выражения (33.5) видно, что E не зависит от расстояния x от заряженной плоскости, т. е.

Следовательно, электрическое поле, создаваемое бесконечной равномерно заряженной плоскостью, является однородным.

Пример 33.2. Имеем равномерно заряженную сферу с поверхностной плотностью заряда σ. Радиус сферы R. Определить напряженн о сть Е электрического поля на расстоянии r от центра сферы.

Дано:   σ   R r	Решение   Сначала определим Е в точке, находящейся внутри заряженной сферы (r < R). Проведем через нее гауссову замкнутую поверхность S в виде сферы радиусом r и с центром в точке О (рис. 33.3). Согласно теореме Гаусса
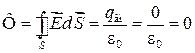
E –?

(из рис. 33.3 видно, что заряда внутри гауссовой поверхности нет), откуда следует, что

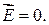
Следовательно, внутри заряженной сферы напряженность Е электрического поля равна нулю.

Теперь определим Е в точке, находящейся вне заряженной сферы (r > R). Пусть сфера заряжена положительно. Вследствие симметрии вектор Е поля, создаваемого сферой, в интересующей нас точке направлен радиально от центра сферы.

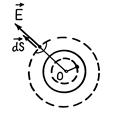Рис. 33.3

Определим модуль (длину) этого вектора. Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде сферы радиусом r и с центром в точке О (рис. 33.3). Найдем поток вектора сквозь гауссову поверхность:

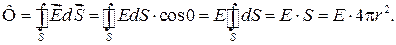(33.6)

При интегрировании мы учли, что для всех точек гауссовой сферы α = 0 и Е = = const.

Согласно теореме Гаусса

(33.7)

Из рис. 33.3 видно, что заряженная сфера находится внутри гауссовой поверхности и поэтому заряд q _вн равен заряду q _сф сферы. В случае равномерно заряженной сферы (σ = const) можем записать

откуда

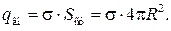(33.8)

Подставляя выражения (33.6) и (33.8) в соотношение (33.7), получаем

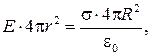
откуда

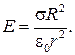(33.9)

Следовательно, напряженность Е поля вне заряженной сферы убывает с расстоянием r. Графически зависимость E (r) электрического поля равномерно заряженной сферы представлена на рис. 33.4.

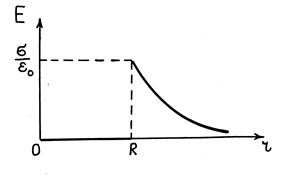
Рис. 33.4

Пример 33.3. Имеем равномерно заряженный шар с объемной плотностью заряда ρ. Радиус шара R. Определить напряженн о сть Е электрического поля на расстоянии r от центра шара.

Дано:   ρ   R r	Решение   Сначала определим Е в точке, находящейся внутри заряженного шара (r < R). Пусть шар заряжен положительно. Вследствие симметрии вектор поля, создаваемого шаром, в интересующей нас точке направлен радиально от центра шара.
E –?

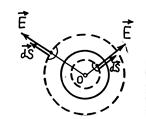Рис. 33.5

Определим модуль (длину) этого вектора. Проведем через интересующую нас точку гауссову замкнутую поверхность S в виде сферы радиусом r и с центром в точке О (рис. 33.5). Найдем поток вектора сквозь гауссову поверхность:

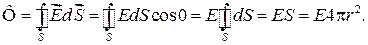(33.10)

При интегрировании мы учли, что для всех точек гауссовой сферы α = 0 и Е = const.

Согласно теореме Гаусса

(33.11)

где 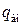— заряд части шара, сосредоточенный внутри гауссовой сферы. Найдем его. По определению, объемная плотность заряда

В случае равномерно заряженного шара (ρ = const) можем написать

(33.12)

где 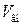— объем шара внутри гауссовой сферы. Из выражения (33.12) находим

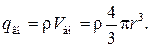(33.13)

Подставляя выражения (33.10) и (33.13) в соотношение (33.11), получаем

откуда

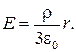(33.14)

Следовательно, напряженность Е поля вне заряженной сферы возрастает с расстоянием r.

Теперь, рассуждая аналогично, определим Е в точке, находящейся вне заряженного шара (r > R). Из рис. 33.5 видно, что весь заряженный шар находится внутри гауссовой поверхности и поэтому q _вн равен заряду q _ш шара. Можем написать

откуда

Из соотношения

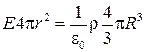
следует

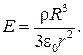(33.15)

Следовательно, напряженность Е поля вне заряженного шара убывает с расстоянием r. Графически зависимость E (r) электрического поля равномерно заряженного шара представлена на рис. 33.6.

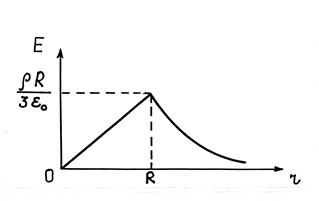
Рис. 33.6

§ 34. Циркуляция вектора

Электрическое поле, создаваемое одним неподвижным точечным зарядом или системой неподвижных точечных зарядов, называют электростатическим. Работа сил этого поля по перемещению заряженной частицы между двумя любыми точками не зависит от траектории перемещения частицы, а зависит только от положения этих точек.

Пусть точечный заряд 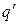= 1 Кл переносится под действием силы 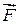электростатического поля из точки 1 в точку 2. Работа силы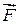

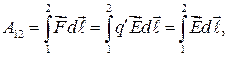(34.1)

где — элементарное перемещение заряда 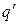, не зависит от траектории движения заряда 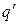. Следовательно, линейный интеграл

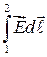
не зависит от формы и длины линии между точками 1 и 2. Интеграл

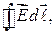
взятый по замкнутой линии (контуру), называют циркуляцией вектора ( — элементарное перемещение вдоль контура). Аналогично определяют циркуляцию любого вектора.

Теорема о циркуляции вектора . Циркуляция вектора в любом электростатическом поле равна нулю:

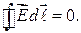(34.2)

Доказательство теоремы. Имеем замкнутый контур 1 a 2 b 1 (рис. 34.1). Циркуляция вектора

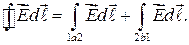(34.3)

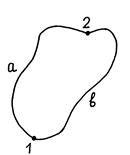Рис. 34.1

Так как 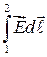не зависит от формы и длины линии, имеем (34.4)

Подставляя выражение (34.3) в соотношение (34.3), получаем

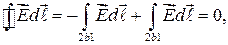
что и требовалось доказать.

Теорема о циркуляции вектора позволяет по линиям вектора определить, электростатическое это поле или нет.

Пример 34.1. Является ли поле, изображенное на рис. 34.2, электростатическим?

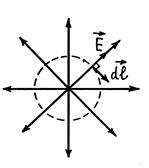Рис. 34.2

Решение. Проведем замкнутый контур в виде окружности с центром, совпадающим с центром поля (пунктирная окружность на рис. 34.2). Будем обходить контур по часовой стрелке. Циркуляция вектора  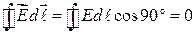 (мы учли, что при интегрировании по контуру угол между векторами и равен ).

Следовательно, согласно теореме о циркуляции вектора , поле, изображенное на рис. 34.2, является электростатическим.

Пример 34.2. Возьмем в качестве замкнутого контура одну из линий вектора . Будем обходить контур по часовой стрелке. Циркуляция вектора

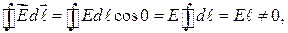
где ℓ — длина контура (мы учли, что при интегрировании по контуру угол между векторами и равен нулю и Е = const).

Следовательно, согласно теореме о циркуляции вектора , поле, изображенное на рис. 34.3, не является электростатическим.

Рис. 34.3

Поиск по сайту: