Уравнение Ван-дер-Ваальса

Уравнение состояния идеального газа (уравнение Клапейрона – Менделеева)

(29.1)

было получено в предположении, что молекулы газа имеют пренебрежимо малый собственный объем, не взаимодействуют друг с другом на расстоянии и сталкиваются между собой как упругие шарики. Очевидно, такое допущение можно делать только для газов при небольших давлениях (~1 атм), когда расстояния между молекулами газа таковы, что силами межмолекулярного взаимодействия можно пренебречь (при 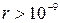м).

Модель газа, отличная от модели идеального газа, была предложена Ван-дер-Ваальсом. Согласно этой модели, молекулы газа имеют собственный объем, взаимно притягиваются друг к другу и сталкиваются между собой как упругие шарики. Такая модель позволила получить уравнение состояния газа, более соответствующее свойствам реальных газов, чем уравнение Клапейрона – Менделеева. Это уравнение, называемое уравнением Ван-дер-Ваальса, имеет вид

(29.2)

где и — постоянные для данного газа величины, которые определяют опытным путем.

Уравнение (29.2) отличается от уравнения (29.1) двумя поправками: и ν b. Поправка учитывает действие молекулярных сил притяжения, которое эквивалентно действию дополнительного давления, испытываемого газом. Величина этого дополнительного давления

(29.3)

Поправка ν b учитывает собственный объем молекул. Она равна учетверенному собственному объему всех молекул газа.

Поиск по сайту: