 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
ГЛАВА 3. ЗАКОНЫ СОХРАНЕНИЯ
§ 7. Механическая энергия.
Закон сохранения механической энергии
Назовем силовым полем (или просто полем) область пространства, в которой в каждой точке на помещенную туда частицу действует сила. Если эта сила перемещает частицу по траектории из точки 1 в точку 2 и при этом ее работа не зависит от пройденного частицей пути, а зависит только положение точек 1 и 2, силу называют консервативной, а поле, где действует такая сила, потенциальным.
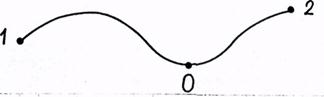
Рис. 7.1
Пусть консервативная сила  перемещает частицу из разных точек
перемещает частицу из разных точек 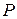 потенциального поля в одну фиксированную точку 0. Работа этой силы будет зависеть только от положения точек
потенциального поля в одну фиксированную точку 0. Работа этой силы будет зависеть только от положения точек 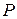 , определяемым радиусом-вектором
, определяемым радиусом-вектором  , или, другими словами, работа является некоторой функцией
, или, другими словами, работа является некоторой функцией 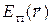 :
:

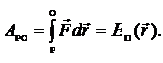 |
(7.1)
Функцию 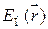 называют потенциальной энергией частицы в данной точке поля.
называют потенциальной энергией частицы в данной точке поля.
Найдем работу силы  при движении частицы из точки 1 в точку 2 по траектории, проходящей через точку 0 (рис. 7.1). Можем написать
при движении частицы из точки 1 в точку 2 по траектории, проходящей через точку 0 (рис. 7.1). Можем написать
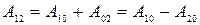
или, с учетом выражения (7.1),
 |
(7.2)
откуда видно, что работа консервативной силы равна убыли потенциальной энергии частицы.
По определению элементарная работа силы 
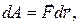
а согласно основному уравнению динамики частицы
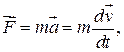
откуда
 (7.3)
(7.3)
Величину
 (7.4)
(7.4)
где  и v — масса и скорость частицы соответственно, называют кинетической энергией частицы.
и v — масса и скорость частицы соответственно, называют кинетической энергией частицы.
Из выражения (7.3)

при движении частицы по траектории из точки 1 в точку 2 получаем
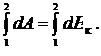
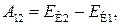 (7.5)
(7.5)
откуда видно, что работа консервативной силы равна приращению кинетической энергии частицы.
В том случае, если частица в потенциальном поле движется под действием консервативной и сторонней (неконсервативной) сил, соотношение (7.5) имеет вид
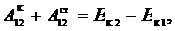 |
(7.6)
где  и
и  — соответственно работы консервативной силы и сторонней силы (например, силы трения).
— соответственно работы консервативной силы и сторонней силы (например, силы трения).
С учетом выражений (7.2) и (7.6), можем записать
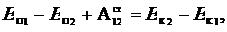

откуда
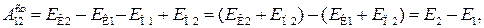 (7.7)
(7.7)
где величину
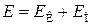 (7.8)
(7.8)
называют механической энергией частицы в потенциальном поле.
В том случае, если на частицы действует только консервативная сила, то в формуле (7.7) 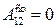 , откуда следует
, откуда следует

или
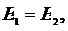 (7.9)
(7.9)
механическая энергия частицы, на которую действует только консервативная сила, остается постоянной (закон сохранения механической энергии):
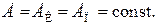 (7.10)
(7.10)
Если сила, действующая на твердое тело, является консервативной, то закон сохранения механической энергии (7.10) справедлив и для твердого тела, вращающегося вокруг неподвижной оси, однако кинетическая энергия вращательного движения будет иметь другой вид, чем (7.4), а именно
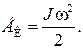 (7.11)
(7.11)
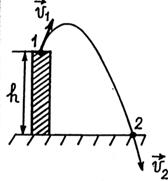
Пример 7.1. Тело массой  бросили со скоростью v 1 с башни высотой
бросили со скоростью v 1 с башни высотой 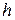 (рис. 7.2). На землю тело упало со скоростью v 2. Найти по этим данным работу A c силы сопротивления воздуха.
(рис. 7.2). На землю тело упало со скоростью v 2. Найти по этим данным работу A c силы сопротивления воздуха.
Дано:
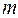 v 1
v 1
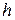
 V 2
V 2
| Решение

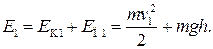
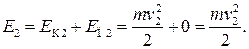 Рис. 7.2
Рис. 7.2
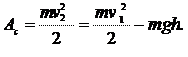
|
| A c –? |
Ответ: 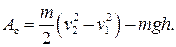
Пример 7.2. Сплошной цилиндр массой 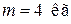 катится без скольжения по горизонтальной поверхности. Скорость оси цилиндра
катится без скольжения по горизонтальной поверхности. Скорость оси цилиндра 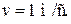 Найти кинетическую энергию
Найти кинетическую энергию 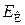 цилиндра.
цилиндра. 

Дано:
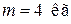
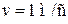
| Решение
Если твердое тело с массой  вращается вокруг оси, проходящей через центр масс тела, который в свою очередь движется поступательно со скоростью v, то кинетическая энергия такого тела вращается вокруг оси, проходящей через центр масс тела, который в свою очередь движется поступательно со скоростью v, то кинетическая энергия такого тела
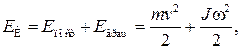  
|
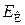 –? –?
|
где 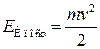 — кинетическая энергия поступательного движения тела;
— кинетическая энергия поступательного движения тела;
 —кинетическая энергия вращательного движения тела.
—кинетическая энергия вращательного движения тела.
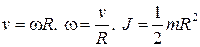 (см. Приложение А).
(см. Приложение А).

Ответ: 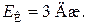
Пример 7.3. Тело бросили со скоростью 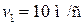 под углом к горизонту. Найти скорость v 2 тела на высоте
под углом к горизонту. Найти скорость v 2 тела на высоте 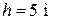 над горизонтом. Сопротивлением воздуха пренебречь.
над горизонтом. Сопротивлением воздуха пренебречь.
Дано:
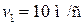
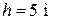
| Решение
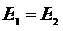 . .
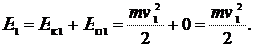
|
| v 2 –? |
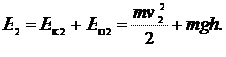
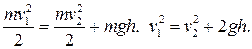
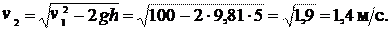
Ответ: 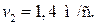
Пример 7.4. Карандаш длиной 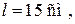 поставленный вертикально, падает на стол. Какую угловую ω и линейную vc скорости будет иметь в конце падения середина карандаша?
поставленный вертикально, падает на стол. Какую угловую ω и линейную vc скорости будет иметь в конце падения середина карандаша?
Дано:
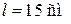 
| Решение
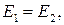
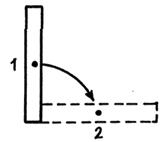 где Е 1 и Е 2 — механическая энергия карандаша в положениях 1 и 2 (рис.
Рис. 7.3
7.3). Ось вращения где Е 1 и Е 2 — механическая энергия карандаша в положениях 1 и 2 (рис.
Рис. 7.3
7.3). Ось вращения 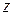 проходит через основание карандаша перпендикулярно плоскости проходит через основание карандаша перпендикулярно плоскости
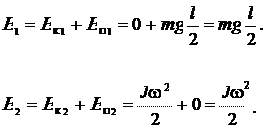  
|
| ω –? vc –? |
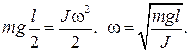
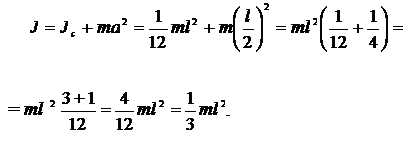
(см. Приложение А)
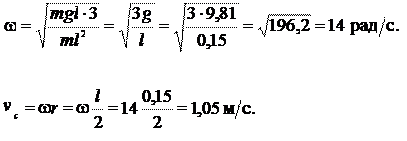
Ответ: 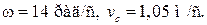
Поиск по сайту: