Магнитная индукция

Если электрические заряды неподвижны, то взаимодействие между ними носит электростатический характер. На каждый точечный заряд q действует электрическая сила

(47.1)

Если электрические заряды движутся, то взаимодействие между ними носит электромагнитный характер. На каждый точечный заряд q, движущийся со скоростью , действует электромагнитная сила

(47.2)

называемая силой Лоренца.

Вторую составляющую силы Лоренца

(47.3)

называют магнитной силой. В связи с этой силой вводят понятие магнитного поля, характеризуемого вектором , называемым магнитной индукцией. Направления векторов , и связаны правилом правого винта (если направить указательный палец правой руки по вектору , а средний — по вектору , то отогнутый большой палец в случае q > 0 покажет направление вектора , а в случае q < 0 — направление, противоположное направлению вектора ) (рис. 47.1).

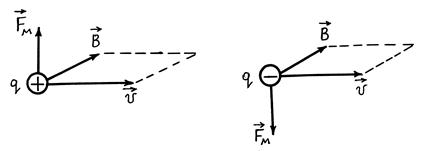
Рис. 47.1

Из рис. 47.1 видно, что вектор перпендикулярен плоскости, в которой лежат векторы и . Модуль магнитной силы

(47.4)

где v и B — модули векторов и ; α — угол между векторами и . При откуда

(47.5)

Следовательно, магнитная индукция — это вектор, модуль которого равен отношению максимальной магнитной силы, действующей на движущийся положительный точечный заряд, к произведению величины q этого заряда на его скорость v, а направление перпендикулярно направлению магнитной силы. Магнитную индукцию измеряют в теслах (Тл).

Опыт показывает, что движущийся со скоростью точечный заряд q создает на расстоянии r от него магнитную индукцию

(47.6)

где μ₀ — магнитная постоянная (); — радиус-вектор, проведенный из начала координат, в котором расположен заряд q, до интересующей нас точки поля. Направления векторов , и связаны правилом правого винта (рис. 47.2). Из рис. 47.2 видно, что конец радиуса-вектора неподвижен, а его начало движется со скоростью . Поэтому магнитная индукция движущегося точечного заряда зависит не только от положения интересующей нас точки, но и от времени.

Рис. 47.2

Из опыта следует, что магнитная индукция системы N движущихся точечных зарядов или токов

(47.7)

где 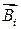— магнитная индукция в интересующей нас точке, создаваемая i -м точечным зарядом или током в отсутствие других точечных зарядов или токов. Соотношение (47.7) выражает принцип суперпозиции магнитных полей.

Стационарное (не изменяющееся со временем) магнитное поле можно представить наглядно с помощью линий вектора , которые проводят следующим образом: 1) касательная к ним в каждой точке совпадает с направлением вектора ; 2) число линий, принизывающих единицу площади поверхности, перпендикулярную линиям (густота линий), равно модулю вектора .

Рис. 47.3

Магнитное поле называют однородным, если в каждой точке поля вектор . Линии вектора такого поля параллельны, и расстояния между ними одинаковы (рис. 47.3).

Пример 47.1. Заряженная частица, прошедшая ускоряющую разность потенциалов , движется в однородном магнитном поле с индукцией по окружности радиусом 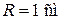. Определить скорость v частицы.

Дано:	Решение   Если заряженная частица с зарядом q влетает со скоростью в однородное магнитное поле перпендикулярно к линиям вектора магнитной индукции , она движется по окружности с постоянной по модулю скоростью под действием магнитной силы
v –?

направленной к центру окружности (рис. 47.4).

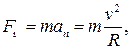где m — масса частицы.

Рис. 47.4

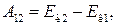где А ₁₂ — работа сил электрического поля по перемещению заряженной частицы из точки 1 в точку 2; — приращение кинетической энергии частицы при этом перемещении. В нашем случае

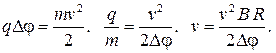
Ответ: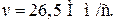

Поиск по сайту: