Угловая скорость и угловое ускорение

Назовем твердым телом систему частиц, расстояния между которыми не меняются в процессе движения.

Рассмотрим вращение твердого тела вокруг неподвижной оси, например оси z, декартовой системы координат. Свяжем направление оси z с положительным направлением отсчета угла поворота φ правилом правого винта (рис. 4.1).

Пусть за элементарный (очень малый) промежуток времени dt тело повернулось вокруг оси z на элементарный угол d φ. Введем вектор модуль которого равен d φ.

Назовем векторную величину

(4.1)

угловой скоростью вращения твердого тела в данный момент времени. Она характеризует быстроту изменения угла поворота тела со временем. Вектор совпадает с направлением вектора .

Проекция угловой скорости на ось z

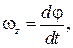(4.2)

производной по времени от угла поворота тела. Если тело вращается в направлении положительного отсчета угла φ (как показано на рис. 4.1), векторы и направлены по оси z и ω _z > 0, в противном случае эти векторы направлены против оси z и ω _z < 0.

Наряду с угловой скоростью вводят еще скалярную величину ν, называемую частотой вращения. Частота вращения показывает, сколько оборотов вокруг оси вращения совершает тело за единицу времени. Очевидно, модуль угловой скорости

(4.3)

Быстроту изменения угловой скорости со временем характеризуют векторной величиной 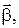называемой векторным ускорением:

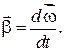(4.4)

Вектор совпадает с направлением вектора — приращением угловой скорости.

Проекция углового ускорения тела на ось z

(4.5)

производной по времени от проекции угловой скорости на ось z.

Если тело вращается ускоренно, направления векторов и совпадают и проекции ω _z и β _z имеют одинаковые знаки. Если тело вращается замедленно, направления векторов и противоположны и проекции ω _z и β _z имеют разные знаки.

Из рис. 4.1 видно, что при вращении частицы твердого тела движутся по различным окружностям, центры которых лежат на оси z. Очевидно, при определенных значениях угловой скорости и углового ускорения твердого тела его частицы имеют различные значения скорости и ускорения. Соответствующий расчет дает возможность установить соотношения между модулями этих величин в зависимости от радиуса r окружности, по которой вращается частица:

(4.6)

(4.7)

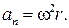(4.8)

Очевидно, для определения угловой скорости и углового ускорения в любой момент времени надо знать закон вращения тела — зависимость φ(t) угла поворота тела от времени.

Пример 4.1. Закон вращения тела где a = 6 рад/с, b = 2 рад/с³. Найти модуль β углового ускорения в момент времени остановки тела.

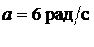
Дано:	Решение             .

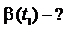
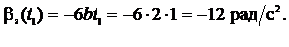
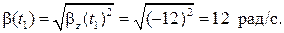
Ответ: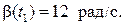

Пример 4.2. Колесо вращается вокруг неподвижной оси z по закону где b = 0,2 рад/с². Найти модуль ускорения частицы на ободе колеса в момент t ₁ =2,5 c, если скорость частицы в этот момент v ₁ = 0,65 м/c.

Дано:	Решение       где R — радиус обода колеса.

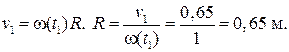
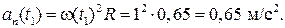
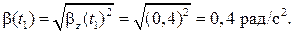
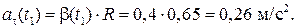
Ответ:

Поиск по сайту: