Гармонические колебания. Пусть частица массой движется под действием упругой силы

Пусть частица массой движется под действием упругой силы

(10.1)

где 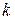— положительная постоянная; и — координата и орт оси .

Согласно основному уравнению динамики частицы,

или в проекциях на ось

(10.2)

Учитывая, что 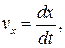перепишем выражение (10.2) в виде дифференциального уравнения

или

(10.3)

где

Решение уравнения (10.3) дает закон движения частицы

(10.4)

называемый гармоническими колебаниями частицы.

Положительную постоянную называют амплитудой колебаний частицы. Она равна максимальному значению координаты частицы . Постоянную ω называют круговой частотой колебаний частицы. Она равна числу колебаний частицы за время, равное 2π, с. Переменную величину называют фазой колебаний частицы, откуда следует, что постоянная α является фазой колебаний в момент 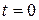и поэтому носит название начальной фазы колебаний частицы

Графически функция (10.4) имеет следующий вид (рис. 10.1).

Рис. 10.1

Из графика видно, что частица при движении периодически пересекает точку , называемую положением равновесия частицы (при ). Кроме того, видно, что через определенный промежуток времени Т значения координаты частицы повторяются. Промежуток времени Т называют периодом колебаний частицы. Можно сказать, что период колебаний — это промежуток времени, за который частица совершает одно колебание.

Назовем частотой νколебаний частицы число колебаний за 1 с. Очевидно,

(10.5)

Единицей измерения частоты является герц (Гц), который равен одному колебанию частицы за 1 с.

Очевидно,

(10.6)

Пример 10.1. Частица массой совершает гармонические колебания вдоль оси с частотой Амплитуда колебаний частицы Определить модуль максимальной силы, действующей на частицу.

Дано:	Решение

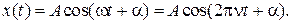
Ответ:

Поиск по сайту: