 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Микрочастица в потенциальном ящике
|
Читайте также: |
Рассмотрим движение микрочастицы в потенциальном поле U (x) при условиях
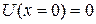 и
и 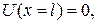 (83.1)
(83.1)
 и
и 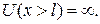 (83.2)
(83.2)
В этом случае говорят, что микрочастица движется в одномерном потенциальном ящике (рис. 83.1).
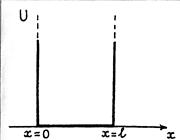 В пределах ящика потенциальная энергия микрочастицы U = 0 и уравнение Шредингера имеет вид
В пределах ящика потенциальная энергия микрочастицы U = 0 и уравнение Шредингера имеет вид
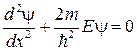 (83.3)
(83.3)
при граничных условиях
Рис. 83.1
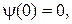 (83.4)
(83.4)
 (83.5)
(83.5)
Обозначим
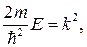 (83.6)
(83.6)
где k — волновое число волны де Бройля для микрочастицы внутри потенциального ящика. Общее решение уравнения
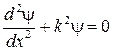
запишем в виде
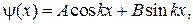
где A и B — постоянные.
Используя граничные условия (83.4) и (83.5), получаем
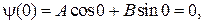
откуда A = 0.
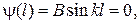
откуда следует, что число k принимает лишь определенные дискретные значения kn, удовлетворяющие условию
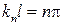
или
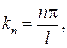 (83.7)
(83.7)
где n = 1, 2, 3, ….
Следовательно, волновая функция внутри потенциального ящика имеет вид
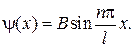 (83.8)
(83.8)
Подставляя выражение (83.7) в соотношение (83.6), получаем очень важный результат:
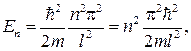 (83.9)
(83.9)
т. е. энергия E микрочастицы в потенциальном ящике не произвольна. Она принимает лишь ряд дискретных собственных значений En.
 Физические величины, принимающие лишь определенные дискретные значения, называются квантованными. Таким образом, энергия микрочастицы, находящейся в потенциальном ящике, является квантованной. Квантованные значения En называют уровнями энергии, а число n, определяющее энергетический уровень микрочастицы, — квантовым числом.
Физические величины, принимающие лишь определенные дискретные значения, называются квантованными. Таким образом, энергия микрочастицы, находящейся в потенциальном ящике, является квантованной. Квантованные значения En называют уровнями энергии, а число n, определяющее энергетический уровень микрочастицы, — квантовым числом.
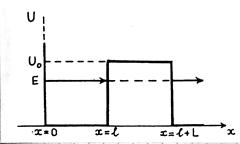
Отметим, что микрочастица, двигаясь в потенциальном ящике с потенциальным барьером конечной высоты U 0, даже имея энергию
E < U 0, может пройти сквозь потенциальный барьер (рис. 83.2). Это явление называют туннельным эффектом. Расчет дает, что вероятность туннельного эффекта
Рис. 83.2
 (83.10)
(83.10)
где L — ширина потенциального барьера.
Туннельный эффект осуществляется только в тех случаях, когда ширина L потенциального барьера соизмерима с атомными размерами. Например, при 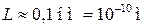 и
и  для электронов с
для электронов с 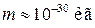
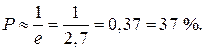
Пример 83.1. Микрочастица находится в одномерном потенциальном ящике шириной l. Вычислить вероятность того, что микрочастица, находящаяся в первом возбужденном состоянии (n = 2), будет обнаружена в средней части ширины ящика.
Дано:
l
n = 2
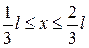
| Решение
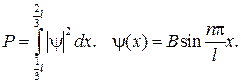 Используя условие нормировки вероятности, найдем B:
Используя условие нормировки вероятности, найдем B:
|
| P –? |

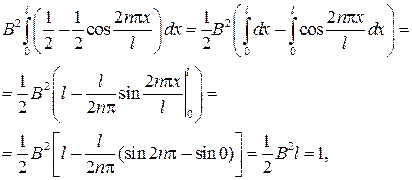
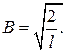
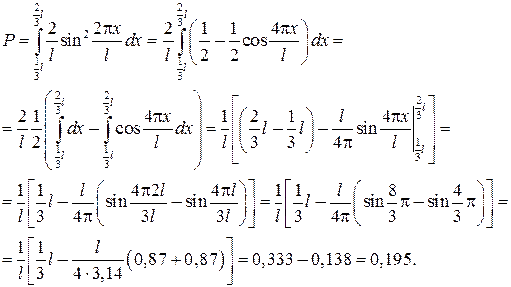
Ответ: P = 0,195.
Поиск по сайту: