Энтропия

Набором макроскопичесих параметров, например, и , задается состояние системы в целом или макросостояние системы. Набор параметров и выражает осредненное суммарное состояние большого числа молекул, из которых состоит система. Назовем микросостоянием системы состояние всех молекул, образующих систему. Состояние каждой молекулы определяется заданием ее координат и скорости в данный момент времени. Очевидно, что микросостояние системы непрерывно меняется. Однако набор макроскопических параметров и , а следовательно, и макросостояние системы при этом может не меняться. Назовем термодинамической вероятностью 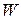число различных микросостояний, соответствующих данному макросостоянию.

Вероятность макросостояния пропорциональна его термодинамической вероятности. Для равновесного состояния системы, при котором параметры 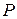, , и остаются неизменными, 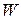имеет максимальное значение по сравнению с любым неравновесным состоянием. Поэтому равновесное состояние наиболее вероятно. Если система переходит из неравновесного состояния в равновесное, то такой процесс необратим.

Определить вероятность состояния через термодинамическую вероятность неудобно, так как 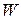не обладает свойством аддитивности (нельзя складывать). Действительно, если мысленно разбить термодинамическую систему на 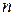подсистем с термодинамическими вероятностями (рис 25.1),

Рис. 25.1

то термодинамическая вероятность системы

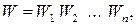(25.1)

откуда видно, что 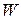не является аддитивной величиной.

Взяв логарифм от соотношения (25.1), получим

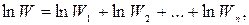
откуда видно, что 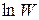— аддитивная величина (можно складывать).

Введем физическую величину

(25.2)

где 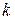— постоянная Больцмана. Величину называют энтропией системы. Она характеризует вероятность макросостояния системы. Определение энтропии (25.2) было сделано Больцманом.

Дадим еще одно определение энтропии. Рассмотрим расширение газа в пустоту (рис. 25.2).

Рис. 25.2

Расчет дает

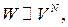
где 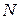— число молекул газа в объеме , или

,

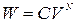где 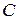— коэффициент пропорциональности.

Очевидно, в нашем случае 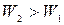, так как . С учетом выражения (25.2) можем написать

откуда приращение энтропии

(25.3)

Учитывая, что и 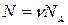, перепишем выражение (25.3) в виде

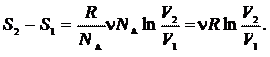(25.4)

При изотермическом увеличении объема газа от 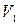до 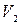при температуре количество тепла, полученное газом,

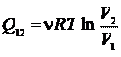(25.5)

(см. пример 23.1). Сравнивая выражение (25.4) и (25.5), получаем

(25.6)

или для элементарного приращения энтропии

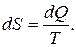
(25.7)

Формула (25.7) верна не только для изотермического процесса, но и для любого равновесного обратимого процесса

(25.8)

Определение энтропии (25.7) было сделано Клаузиусом.

Из выражений (25.2) и (25.6) следует, что энтропия является функцией состояния системы.

Пример 25.1. Определить приращение энтропии 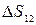при изотермическом кислороде массой M = 10 г от объема V ₁ = 25 л до объема V ₂ = 100 л.

Дано:   M = 10 г   V 1 = 25 л   V 2 = 100 л	Решение

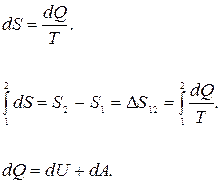
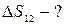
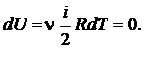
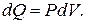
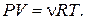
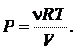
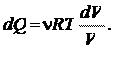
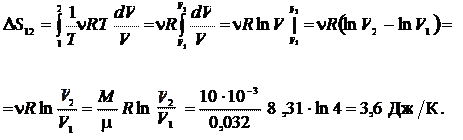
Ответ:

Пример 25.2. Пять молей гелия изохорически переводят из состояния, в котором его давление 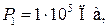в состояние, в котором его давление 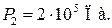Определить приращение энтропии 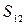гелия.

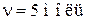
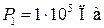
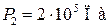
Дано:	Решение

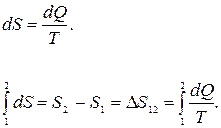
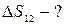
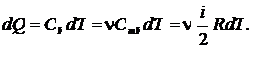
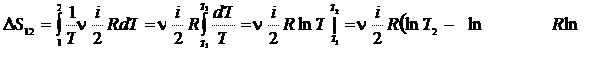
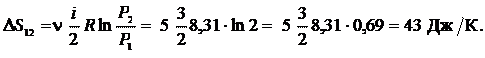
Ответ: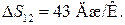

Поиск по сайту: