Распределение Больцмана

Барометрическая формула (18.4) позволяет найти зависимость числа молекул 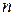в единице объема газа от высоты 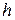над земной поверхностью. По-прежнему будем считать, что газ находится в равновесном состоянии при температуре в однородном гравитационном поле ().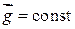

Из уравнения Клапейрона – Менделеева следует

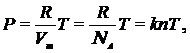(19.1)

где 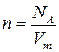— число молекул газа в единице объема.

Подставим выражение (19.1) в барометрическую формулу, имеем

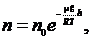
(19.2)

где 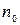— число молекул в единице объема газа при .

Можем написать

(19.3)

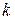где — масса молекулы; — постоянная Больцмана.

Подставляем формулу (19.3) в соотношение (19.2), получаем

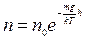
(19.4)

или

(19.5)

где — потенциальная энергия молекулы газа в гравитационном поле Земли.

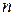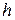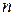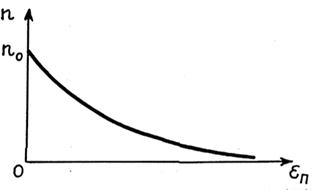
Следовательно, найденная зависимость (19.4) от переходит в зависимость (19.5) от 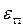(рис. 19.1), согласно которой в объеме газа молекул будет больше там, где их потенциальная энергия меньше.

Рис. 19.1

Больцман доказал, что распределение (19.5) справедливо не только для молекул газа в потенциальном гравитационном поле Земли, но и для совокупности любых одинаковых хаотически движущихся частиц в любом потенциальном силовом поле. Поэтому распределение (19.5) называют распределение Больцмана.

Пример 19.1. Пусть η₀ — отношение концентрации молекул водорода к концентрации молекул азота вблизи поверхности Земли, а η — соответствующее отношение на высоте h = 3 км. Найти отношение η/η₀ при Т = 280 К, полагая, что температура и ускорение свободного падения не зависят от высоты.

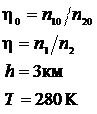
Дано:	Решение
η/η0 –?

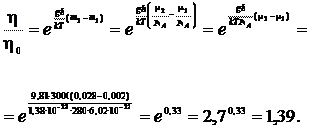
Ответ: η/η₀ = 1,39.

Поиск по сайту: