Вопрос 1 Равномерное и показательное распределение

Непрерывная случайная величина Х имеет равномерноераспределение на отр {a;b}, если на этом отрезке плотность распределения вероятности случайной величины постоянна, т.е. если дифференцируемая ф-я распределения f(x) имеет вид f(x)={0, х≤a; С, a<x≤b; 0, x>b}, здесь С=1/(b-a), далее из формулы f(x) заменяем С на соответствующее выражение. Тогда искомая функция F(x)={0, х≤a; (x-a)/(b-a), a<x≤b; 1, x>b}

Мат ожидание случ величины распределенной равномерно М(х)=(b+a)/2. D(x)=(b-a)² /12. с.к.о. =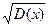

Непрерывная случайная величина Х, ф-я и плотность которой заданы выражением f(x)= называется случайная величина, имеющая показательное (экспоненциальное) распределение.Ф-я распределения этого закона имеет вид: F(x)= . М(х)=1, D(x)= 1/λ², Ϭ(х)= 1/λ.

Поиск по сайту: